Business and Data Analytics

 What is Data Visualization?

Data visualization translates complex data sets into visual formats that are easier for the human brain to comprehend. This can include a variety of visual tools such as:

• Charts: Bar charts, line charts, pie charts, etc.
• Graphs: Scatter plots, histograms, etc.
• Maps: Geographic maps, heat maps, etc.
• Dashboards: Interactive platforms that combine multiple visualizations.

The primary goal of data visualization is to make data more accessible and easier to interpret, allowing users to identify patterns, trends, and outliers quickly. 

Types of Data for Visualization

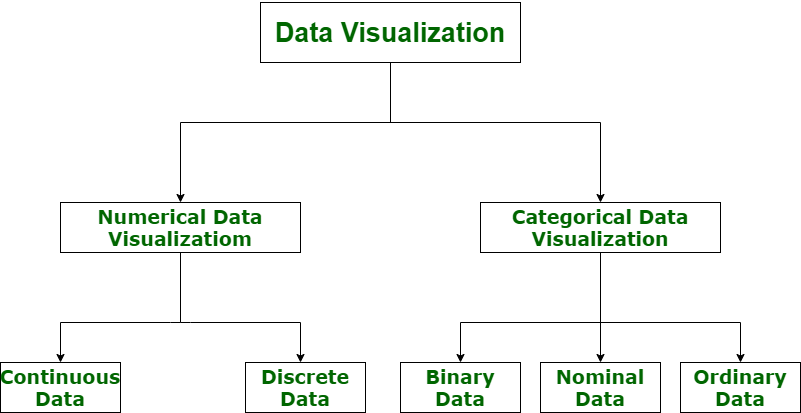
Data visualization is categorized into the following categories:

• Numerical Data 
• Categorical Data

Let’s understand the visualization of data via a diagram with its all categories.

Why is Data Visualization Important?

Let’s take an example. Suppose you compile visualization data of the company’s profits from 2013 to 2023 and create a line chart. It would be very easy to see the line going constantly up with a drop in just 2018. So you can observe in a second that the company has had continuous profits in all the years except a loss in 2018.

It would not be that easy to get this information so fast from a data table. This is just one demonstration of the usefulness of data visualization. Let’s see some more reasons why visualization of data is so important.

1. Data Visualization Discovers the Trends in Data

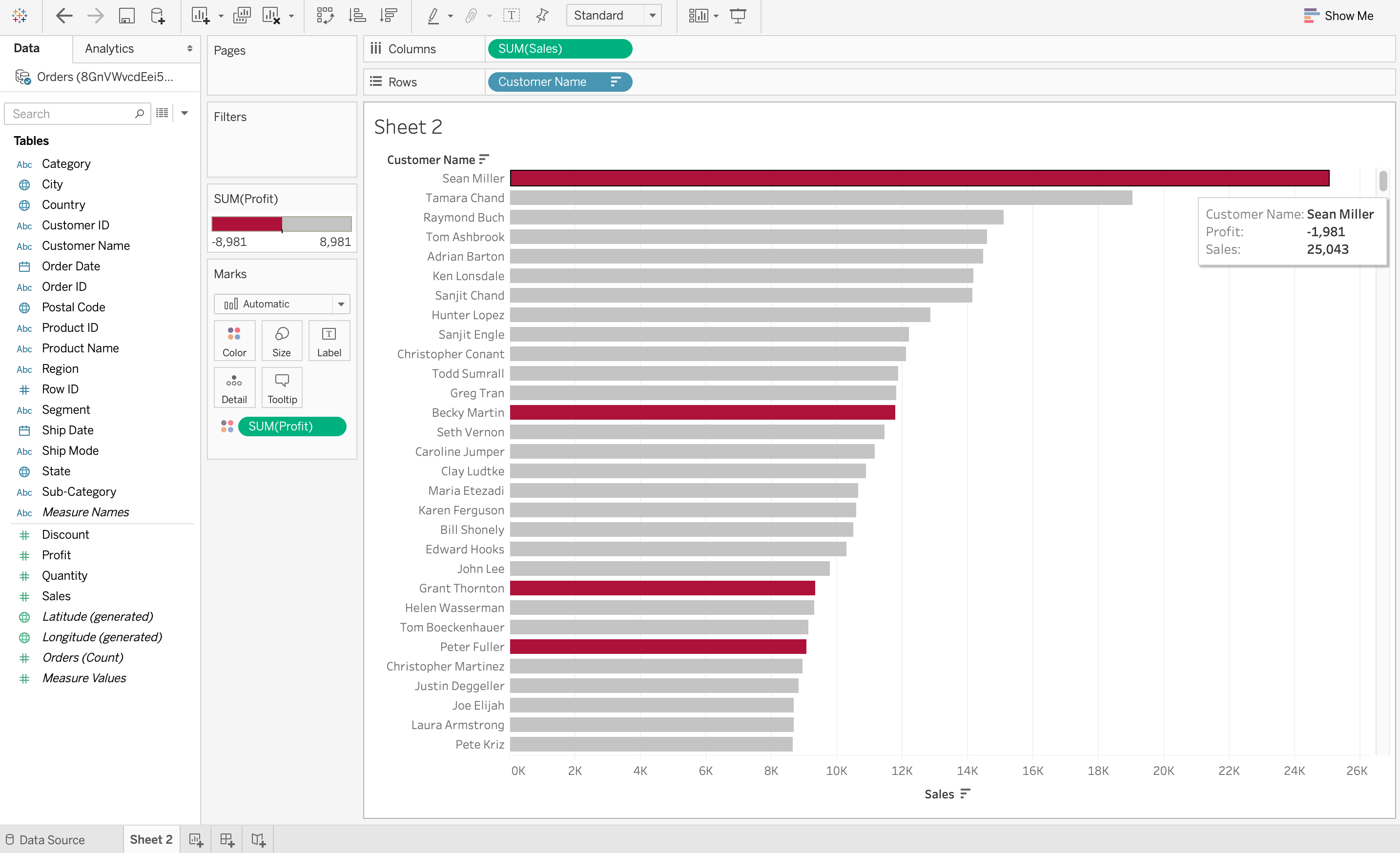
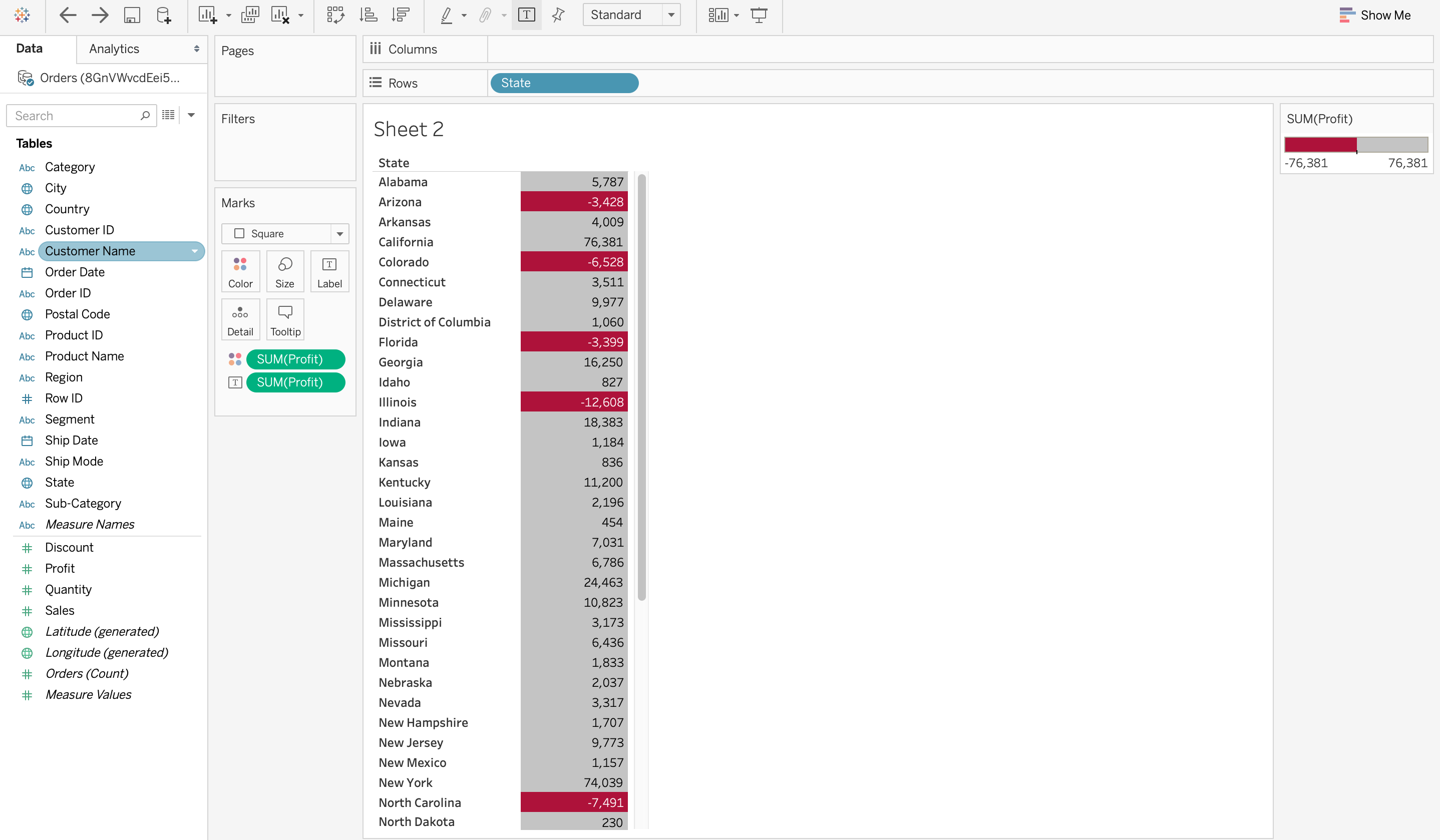
The most important thing that data visualization does is discover the trends in data. After all, it is much easier to observe data trends when all the data is laid out in front of you in a visual form as compared to data in a table. For example, the screenshot below on visualization on Tableau demonstrates the sum of sales made by each customer in descending order. However, the color red denotes loss while grey denotes profits. So it is very easy to observe from this visualization that even though some customers may have huge sales, they are still at a loss. This would be very difficult to observe from a table.

2. Data Visualization Provides a Perspective on the Data

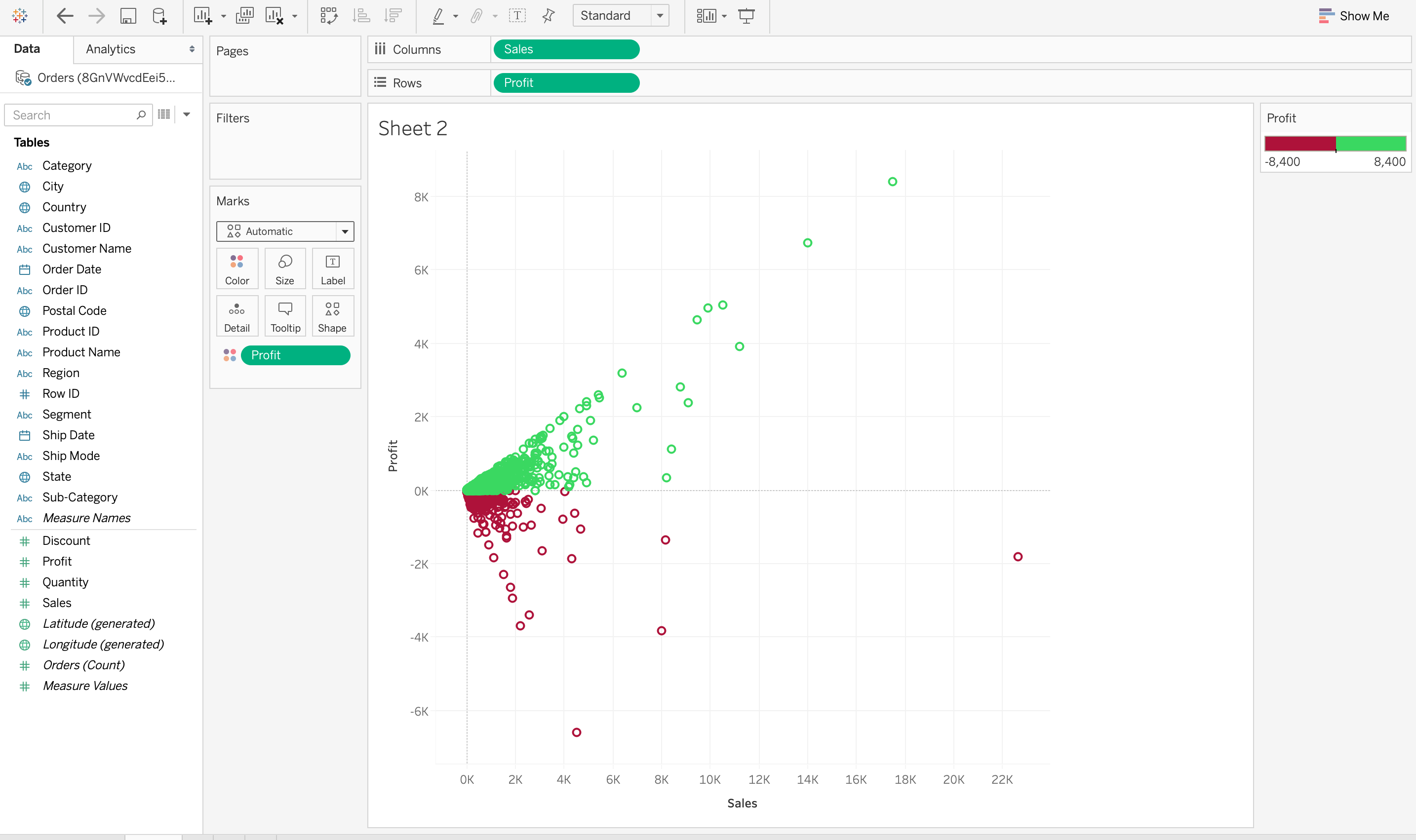
Visualizing Data provides a perspective on data by showing its meaning in the larger scheme of things. It demonstrates how particular data references stand concerning the overall data picture. In the data visualization below, the data between sales and profit provides a data perspective concerning these two measures. It also demonstrates that there are very few sales above 12K and higher sales do not necessarily mean a higher profit.

3. Data Visualization Puts the Data into the Correct Context

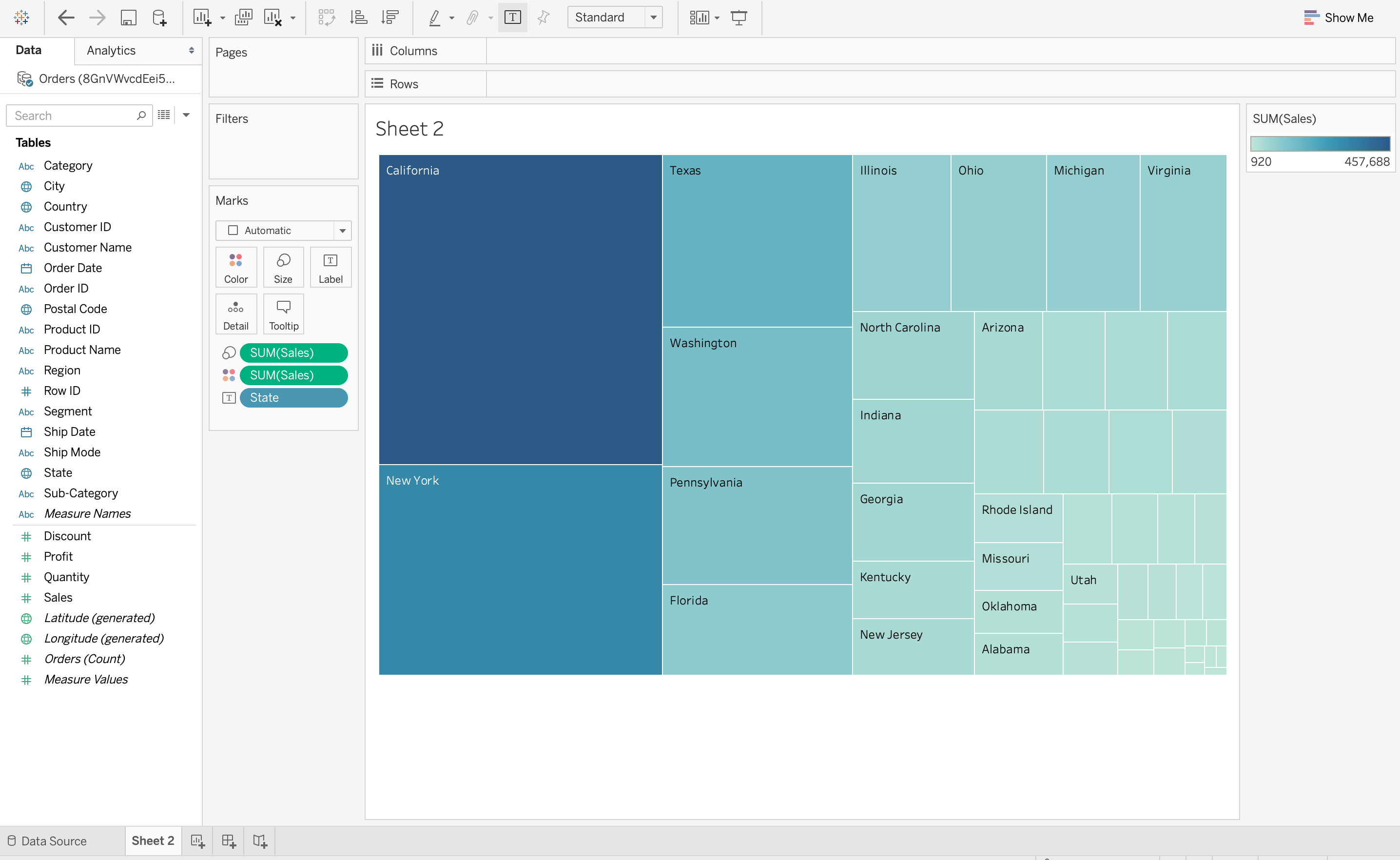
It isn’t easy to understand the context of the data with data visualization. Since context provides the whole circumstances of the data, it is very difficult to grasp by just reading numbers in a table. In the below data visualization on Tableau, a TreeMap is used to demonstrate the number of sales in each region of the United States. It is very easy to understand from this data visualization that California has the largest number of sales out of the total number since the rectangle for California is the largest. But this information is not easy to understand outside of context without visualizing data.

4. Data Visualization Saves Time

It is definitely faster to gather some insights from the data using data visualization rather than just studying a chart. In the screenshot below on Tableau, it is very easy to identify the states that have suffered a net loss rather than a profit. This is because all the cells with a loss are coloured red using a heat map, so it is obvious states have suffered a loss. Compare this to a normal table where you would need to check each cell to see if it has a negative value to determine a loss. Visualizing Data can save a lot of time in this situation!

5. Data Visualization Tells a Data Story

Data visualization is also a medium to tell a data story to the viewers. The visualization can be used to present the data facts in an easy-to-understand form while telling a story and leading the viewers to an inevitable conclusion. This data story, like any other type of story, should have a good beginning, a basic plot, and an ending that it is leading towards. For example, if a data analyst has to craft a data visualization for company executives detailing the profits of various products, then the data story can start with the profits and losses of multiple products and move on to recommendations on how to tackle the losses.

Now, that we have understood the basics of Data Visualization, along with its importance, now will be discussing the Advantages, Disadvantages and Data Science Pipeline (along with the diagram) which will help you to understand how data is compiled through various checkpoints.

Types of Data Visualization Techniques

Various types of visualizations cater to diverse data sets and analytical goals.

1. Bar Charts: Ideal for comparing categorical data or displaying frequencies, bar charts offer a clear visual representation of values.
2. Line Charts: Perfect for illustrating trends over time, line charts connect data points to reveal patterns and fluctuations.
3. Pie Charts: Efficient for displaying parts of a whole, pie charts offer a simple way to understand proportions and percentages.
4. Scatter Plots: Showcase relationships between two variables, identifying patterns and outliers through scattered data points.
5. Histograms: Depict the distribution of a continuous variable, providing insights into the underlying data patterns.
6. Heatmaps: Visualize complex data sets through color-coding, emphasizing variations and correlations in a matrix.
7. Box Plots: Unveil statistical summaries such as median, quartiles, and outliers, aiding in data distribution analysis.
8. Area Charts: Similar to line charts but with the area under the line filled, these charts accentuate cumulative data patterns.
9. Bubble Charts: Enhance scatter plots by introducing a third dimension through varying bubble sizes, revealing additional insights.
10. Treemaps: Efficiently represent hierarchical data structures, breaking down categories into nested rectangles.
11. Violin Plots: Violin plots combine aspects of box plots and kernel density plots, providing a detailed representation of the distribution of data.
12. Word Clouds: Word clouds are visual representations of text data where words are sized based on their frequency.
13. 3D Surface Plots: 3D surface plots visualize three-dimensional data, illustrating how a response variable changes in relation to two predictor variables.
14. Network Graphs: Network graphs represent relationships between entities using nodes and edges. They are useful for visualizing connections in complex systems, such as social networks, transportation networks, or organizational structures.
15. Sankey Diagrams: Sankey diagrams visualize flow and quantity relationships between multiple entities. Often used in process engineering or energy flow analysis.

Visualization of data not only simplifies complex information but also enhances decision-making processes. Choosing the right type of visualization helps to unveil hidden patterns and trends within the data, making informed and impactful conclusions.

Tools for Visualization of Data

The following are the 10 best Data Visualization Tools

1. Tableau
2. Looker
3. Zoho Analytics
4. Sisense
5. IBM Cognos Analytics
6. Qlik Sense
7. Domo
8. Microsoft Power BI
9. Klipfolio
10. SAP Analytics Cloud

Advantages and Disadvantages of Data Visualization

Advantages of Data Visualization:

• Enhanced Comparison: Visualizing performances of two elements or scenarios streamlines analysis, saving time compared to traditional data examination.
• Improved Methodology: Representing data graphically offers a superior understanding of situations, exemplified by tools like Google Trends illustrating industry trends in graphical forms.
• Efficient Data Sharing: Visual data presentation facilitates effective communication, making information more digestible and engaging compared to sharing raw data.
• Sales Analysis: Data visualization aids sales professionals in comprehending product sales trends, identifying influencing factors through tools like heat maps, and understanding customer types, geography impacts, and repeat customer behaviors.
• Identifying Event Relations: Discovering correlations between events helps businesses understand external factors affecting their performance, such as online sales surges during festive seasons.
• Exploring Opportunities and Trends: Data visualization empowers business leaders to uncover patterns and opportunities within vast datasets, enabling a deeper understanding of customer behaviors and insights into emerging business trends.

Disadvantages of Data Visualization:

• Can be time-consuming: Creating visualizations can be a time-consuming process, especially when dealing with large and complex datasets.
• Can be misleading: While data visualization can help identify patterns and relationships in data, it can also be misleading if not done correctly. Visualizations can create the impression of patterns or trends that may not exist, leading to incorrect conclusions and poor decision-making.
• Can be difficult to interpret: Some types of visualizations, such as those that involve 3D or interactive elements, can be difficult to interpret and understand.
• May not be suitable for all types of data: Certain types of data, such as text or audio data, may not lend themselves well to visualization. In these cases, alternative methods of analysis may be more appropriate.
• May not be accessible to all users: Some users may have visual impairments or other disabilities that make it difficult or impossible for them to interpret visualizations. In these cases, alternative methods of presenting data may be necessary to ensure accessibility.

Best Practices for Visualization Data

Effective data visualization is crucial for conveying insights accurately. Follow these best practices to create compelling and understandable visualizations:

1. Audience-Centric Approach: Tailor visualizations to your audience’s knowledge level, ensuring clarity and relevance. Consider their familiarity with data interpretation and adjust the complexity of visual elements accordingly.
2. Design Clarity and Consistency: Choose appropriate chart types, simplify visual elements, and maintain a consistent color scheme and legible fonts. This ensures a clear, cohesive, and easily interpretable visualization.
3. Contextual Communication: Provide context through clear labels, titles, annotations, and acknowledgments of data sources. This helps viewers understand the significance of the information presented and builds transparency and credibility.
4. Engaging and Accessible Design: Design interactive features thoughtfully, ensuring they enhance comprehension. Additionally, prioritize accessibility by testing visualizations for responsiveness and accommodating various audience needs, fostering an inclusive and engaging experience.

Use-Cases and Applications of Data Visualization

1. Business Intelligence and Reporting

In the realm of Business Intelligence and Reporting, organizations leverage sophisticated tools to enhance decision-making processes. This involves the implementation of comprehensive dashboards designed for tracking key performance indicators (KPIs) and essential business metrics. Additionally, businesses engage in thorough trend analysis to discern patterns and anomalies within sales, revenue, and other critical datasets. These visual insights play a pivotal role in facilitating strategic decision-making, empowering stakeholders to respond promptly to market dynamics.

2. Financial Analysis

Financial Analysis in the corporate landscape involves the utilization of visual representations to aid in investment decision-making. Visualizing stock prices and market trends provides valuable insights for investors. Furthermore, organizations conduct comparative analyses of budgeted versus actual expenditures, gaining a comprehensive understanding of financial performance. Visualizations of cash flow and financial statements contribute to a clearer assessment of overall financial health, aiding in the formulation of robust financial strategies.

3. Healthcare

Within the Healthcare sector, the adoption of visualizations is instrumental in conveying complex information. Visual representations are employed to communicate patient outcomes and assess treatment efficacy, fostering a more accessible understanding for healthcare professionals and stakeholders. Moreover, visual depictions of disease spread and epidemiological data are critical in supporting public health efforts. Through visual analytics, healthcare organizations achieve efficient allocation and utilization of resources, ensuring optimal delivery of healthcare services.

4. Marketing and Sales

In the domain of Marketing and Sales, data visualization becomes a powerful tool for understanding customer behavior. Segmentation and behavior analysis are facilitated through visually intuitive charts, providing insights that inform targeted marketing strategies. Conversion funnel visualizations offer a comprehensive view of the customer journey, enabling organizations to optimize their sales processes. Visual analytics of social media engagement and campaign performance further enhance marketing strategies, allowing for more effective and targeted outreach.

5. Human Resources

Human Resources departments leverage data visualization to streamline processes and enhance workforce management. The development of employee performance dashboards facilitates efficient HR operations. Workforce demographics and diversity metrics are visually represented, supporting inclusive practices within organizations. Additionally, analytics for recruitment and retention strategies are enhanced through visual insights, contributing to more effective talent management.

Basic Charts for Data Visualization

Basic charts function foundational tools in information visualization, offering trustworthy insights into datasets. Best data visualization charts are:

• Bar Chart
• Line Chart
• Pie Chart
• Scatter Plot
• Histogram

These basic charts are the basis for deeper data analysis and are vital for conveying statistics correctly. 

1. Bar Charts

Bar charts are one of the common visualization tool, used to symbolize and compare express facts by way of showing square bars. A bar chart has X and Y Axis where the X Axis represents one data and the Y axis represents another data. The top of the bar represents the title. Longer bars suggest better values.

There are various types of Bar charts like horizontal bar chart, Stacked bar chart, Grouped bar chart and Diverging bar Chart.

When to Use Bar Chart:

• Comparing Categories: Showcasing contrast among distinct categories to evaluate, summarize or discover relationship in the information.
• Ranking: When we’ve got records with categories that need to be ranked with highest to lowest.
• Relationship between categories: When you have a dataset with multiple specific variables, bar chart can help to display courting between them, to discover patterns and tendencies.

2. Line Charts

Line chart or Line graph is used to symbolize facts through the years series. It presentations records as a series of records points called as markers, connected with the aid of line segments showing the between values over the years. This chart is normally used to evaluate developments, view patterns or examine charge moves.

When to Use Line Chart:

• Line charts can be used to analyze developments over individual values.
• Line charts also are utilized in comparing trends among more than one facts series.
• Line chart is high-quality used for time series information.

3. Pie Charts

A pie chart is a round records visualization tool, this is divided into slices to symbolize numerical percentage or percentages of an entire. Each slice in pie chart corresponds to a category in the dataset and the perspective of the slice is proportional to the share it represents. Pie charts are only valid with small variety of categories. Simple Pie chart and Exploded Pie charts are distinctive varieties of Pie charts.

When to Use Pie Chart:

• Pie charts are used to show specific facts to expose the proportion of elements to the whole. It is used to depict how exclusive classes make up a total pleasant.
• Useful in eventualities where statistics has small range of classes.
• Useful in emphasizing a particular category by way of highlighting a dominant slice.

4. Scatter Chart (Plots)

A scatter chart or scatter plot chart is a effective information visualization device, makes use of dots to symbolize information factors. Scatter chart is used to display and examine variables which enables find courting between the ones variables. Scatter chart uses axes, X and Y. X-Axis represents one numerical variable and Y-axis represents another numerical variable. The variable on X-axis is independent and plotted against the dependent variable in Y-axis. Type of scatter chart consists of simple scatter chart, scatter chart with trendline and scatter chart with coloration coding.

When to Use Scatter Chart:

• Scatter charts are awesome for exploring dating between numerical variables and in identifying traits, outliers and subgroup variations.
• It is used while we’ve got to plot two sets of numerical statistics as one collection of X and Y coordinates.
• Scatter charts are satisfactory used for identifying outliers or unusual remark for your facts.

5. Histogram

A histogram represents the distribution of numerical facts by using dividing it into periods (packing containers) and displaying the frequency of records as bars. It is commonly used to visualize the underlying distribution of a dataset and discover styles inclusive of skewness, valuable tendency, and variability. Histograms are treasured gear for exploring facts distributions, detecting outliers, and assessing records great.

When to Use Histogram:

• Distribution Visualization: Histograms are best for visualizing the distribution of numerical information, allowing customers to recognize the unfold and shape of the records.
• Data Exploration: They facilitate records exploration by using revealing patterns, trends, and outliers inside datasets, aiding in hypothesis generation and information-pushed decision-making.
• Quality Control: Histograms assist assess statistics first-class by way of identifying anomalies, errors, or inconsistencies inside the facts distribution, enabling facts validation and cleaning strategies.

Advanced Charts for Data Visualization

Different types of data visualization charts, offer advanced charts that provide customers, many powerful tools to explore complicated datasets and extract precious insights. These superior charts empowers to analyze, interpret, and understand complex information structures and relationships efficiently.

• Heatmap
• Area Chart
• Box Plot (Box-and-Whisker Plot)
• Bubble Chart
• Tree Map
• Parallel Coordinates
• Choropleth Map
• Sankey Diagram
• Radar Chart (Spider Chart)
• Network Graph
• Donut Chart
• Gauge Chart
• Sunburst Chart
• Hexbin Plot
• Violin Plot

1. Heatmap

A heatmap visualizes statistics in a matrix layout the usage of colors to symbolize the values of person cells. It is good for figuring out patterns, correlations, and variations within big datasets. Heatmaps are usually utilized in fields together with finance for portfolio analysis, in biology for gene expression analysis, and in advertising for customer segmentation.

When to Use heatmap:

• Identify Clusters: Heatmaps help become aware of clusters or groups inside datasets, helping in segmentation and concentrated on techniques.
• Correlation Analysis: They are useful for visualizing correlations between variables, assisting to discover relationships and traits.
• Risk Assessment: Heatmaps are precious for chance assessment, which include figuring out high-hazard regions in monetary portfolios or detecting anomalies in community visitors.

2. Area Chart

An area chart displays data trends over time by filling the area beneath lines. It is effective for illustrating cumulative adjustments and comparing multiple classes simultaneously. Area charts are typically utilized in finance for monitoring stock prices, in weather technological know-how for visualizing temperature developments, and in challenge control for monitoring development through the years.

When to Use Area charts:

• Tracking Trends: Area charts are appropriate for tracking traits and adjustments over time, making them precious for historic records evaluation.
• Comparative Analysis: They permit for clean contrast of multiple classes or variables over the equal time period.
• Highlighting Patterns: Area charts assist spotlight styles, such as seasonality or cyclical tendencies, in time-collection facts.

3. Box Plot (Box-and-Whisker Plot)

A box plot provides a concise precis of the distribution of numerical facts, such as quartiles, outliers, and median values. It is beneficial for identifying variability, skewness, and capacity outliers in datasets. Box plots are typically utilized in statistical analysis, exceptional manipulate, and statistics exploration.

When to Use Box Plots:

• Identify Outliers: Box plots assist discover outliers and extreme values within datasets, helping in information cleansing and anomaly detection.
• Compare Distributions: They permit contrast of distributions between specific groups or categories, facilitating statistical analysis.
• Visualize Spread: Box plots visualize the spread and variability of information, providing insights into the distribution’s form and traits.

4. Bubble Chart

A bubble chart represents records points as bubbles, in which the dimensions and/or colour of every bubble deliver additional facts. It is powerful for visualizing three-dimensional facts and comparing more than one variables simultaneously. Bubble charts are commonly used in finance for portfolio evaluation, in marketing for market segmentation, and in biology for gene expression evaluation.

When to Use bubble chart:

• Multivariate Analysis: Bubble charts permit for multivariate evaluation, permitting the contrast of 3 or greater variables in a unmarried visualization.
• Size and Color Encoding: They leverage size and coloration encoding to deliver extra information, such as fee or class, enhancing records interpretation.
• Relationship Visualization: Bubble charts help visualize relationships between variables, facilitating pattern identification and fashion analysis.

5. Tree Map

A tree map presentations hierarchical facts the usage of nested rectangles, where the size of each rectangle represents a quantitative price. It is effective for visualizing hierarchical systems and comparing proportions in the hierarchy. Tree maps are generally utilized in finance for portfolio evaluation, in facts visualization for displaying report listing systems, and in advertising and marketing for visualizing marketplace share.

When to Use Tree Map:

• Hierarchical Representation: Tree maps excel at representing hierarchical records structures, making them suitable for visualizing organizational hierarchies or nested classes.
• Proportion Comparison: They permit comparison of proportions inside hierarchical systems, aiding in expertise relative sizes and contributions.
• Space Efficiency: Tree maps optimize area utilization by using packing rectangles efficiently, taking into account the visualization of large datasets in a compact layout.

6. Parallel Coordinates

Parallel coordinates visualize multivariate statistics through representing every information point as a line connecting values across multiple variables. They are useful for exploring relationships among variables and figuring out styles or trends. Parallel coordinates are generally used in data evaluation, gadget learning, and sample popularity.

When to Use Parallel Coordinates:

• Multivariate Analysis: Parallel coordinates enable the analysis of multiple variables simultaneously, facilitating sample identification and fashion evaluation.
• Relationship Visualization: They help visualize relationships among variables, such as correlations or clusters, making them precious for exploratory records analysis.
• Outlier Detection: Parallel coordinates resource in outlier detection by identifying facts factors that deviate from the general sample, assisting in anomaly detection and statistics validation.

7. Choropleth Map

A choropleth map uses shade shading or styles to symbolize statistical records aggregated over geographic regions. It is generally used to visualize spatial distributions or variations and identify geographic patterns. Choropleth maps are broadly used in fields which includes demography for populace density mapping, in economics for income distribution visualization, and in epidemiology for disease prevalence mapping.

When to Use Choropleth Map:

• Spatial Analysis: Choropleth maps are best for spatial analysis, permitting the visualization of spatial distributions or variations in records.
• Geographic Patterns: They help become aware of geographic styles, which include clusters or gradients, in datasets, aiding in fashion analysis and decision-making.
• Comparison Across Regions: Choropleth maps allow for clean evaluation of information values throughout one of a kind geographic regions, facilitating local evaluation and coverage planning.

8. Sankey Diagram

A Sankey diagram visualizes the flow of facts or assets among nodes the use of directed flows and varying widths of paths. It is useful for illustrating complex structures or methods and figuring out drift patterns or bottlenecks. Sankey diagrams are typically utilized in power glide evaluation, in deliver chain control for visualizing material flows, and in net analytics for consumer float evaluation.

When to Use Sankey Diagram:

• Flow Visualization: Sankey diagrams excel at visualizing the float of information or resources among nodes, making them valuable for information complex structures or processes.
• Bottleneck Identification: They help perceive bottlenecks or regions of inefficiency within structures by using visualizing flow paths and magnitudes.
• Comparative Analysis: Sankey diagrams permit evaluation of go with the flow patterns between distinct scenarios or time periods, assisting in overall performance evaluation and optimization.

9. Radar Chart (Spider Chart)

A radar chart shows multivariate information on a two-dimensional aircraft with a couple of axes emanating from a primary point. It is beneficial for comparing a couple of variables across distinct categories and identifying strengths and weaknesses. Radar charts are usually utilized in sports for overall performance analysis, in market studies for emblem perception mapping, and in selection-making for multi-criteria decision evaluation.

When to Use Radar Chart:

• Multi-Criteria Comparison: Radar charts permit for the evaluation of more than one criteria or variables across extraordinary classes, facilitating choice-making and prioritization.
• Strengths and Weaknesses Analysis: They assist discover strengths and weaknesses within categories or variables with the aid of visualizing their relative overall performance.
• Pattern Recognition: Radar charts useful resource in pattern recognition via highlighting similarities or variations between classes, assisting in fashion analysis and strategy development.

10. Network Graph

A network graph represents relationships between entities as nodes and edges. It is useful for visualizing complicated networks, consisting of social networks, transportation networks, and organic networks. Network graphs are typically utilized in social network analysis for community detection, in community safety for visualizing community traffic, and in biology for gene interaction analysis.

When to Use Network Graph:

• Relationship Visualization: Network graphs excel at visualizing relationships among entities, which includes connections or interactions, making them valuable for network analysis and exploration.
• Community Detection: They assist discover communities or clusters within networks by using visualizing node connections and densities.
• Path Analysis: Network graphs resource in route analysis by means of visualizing shortest paths or routes among nodes, facilitating course optimization and navigation.

11. Donut or Doughnut chart

A donut chart additionally known as doughnut chart is just like pie chart, but with a blank middle, which offers the arrival of a doughnut. This graphical view offers more aesthetically eye-catching and less cluttered illustration of multiple classes in a dataset.

The ring in the donut chart represents 100% and every class of records is represented with the aid of every slice. The region of every slice indicates how special categories make up a complete amount.

When to Use Donut Chart:

• The donut charts are useful in showing income figures, market proportion or to demonstrate marketing marketing campaign effects, customer segmentation or in similar use instances.
• Used to focus on a single variable and its progress.
• Useful to display components of a whole, showing how person classes make a contribution to an common total.
• Best used for comparing few classes.

12. Gauge Chart

A Gauge chart, one of the visualization tool used to show the progress of a single fee of statistics or key overall performance indicator (KPI) in the direction of a purpose or goal value. The Gauge chart usually displayed like a speedometer which displays facts in a circular arc. There two different kinds of Gauge charts specifically Circular Gauge or Radial Gauge which resembles a speedometer and Linear Gauge.

When to Use Gauge Chart:

Uses of Gauge charts include Goal Achievement, Monitoring Performance, Real-Time Updates and Visualizing Progress.

• Useful in monitoring metrics like income or consumer satisfaction towards benchmark signs set.
• Used in KPI monitoring in tracking development towards a selected aim indicator.
• Can be utilized in project control to music the fame of project progress against assignment timeline.

13. Sunburst Chart

A sunburst chart presents hierarchical records using nested rings, in which each ring represents a degree within the hierarchy. It is beneficial for visualizing hierarchical structures with more than one tiers of aggregation. Sunburst charts permit customers to explore relationships and proportions inside complicated datasets in an interactive and intuitive way.

When to use sunburst charts:

• Visualizing hierarchical data systems, including organizational hierarchies or nested classes.
• Exploring relationships and proportions within multi-level datasets.
• Communicating complex records structures and dependencies in a visually attractive layout.

14. Hexbin Plot

A hexbin plot represents the distribution of dimensional facts by using binning records points into hexagonal cells and coloring each cellular based totally on the range of factors it contains. It is effective for visualizing density in scatter plots with a huge wide variety of information points. Hexbin plots provide insights into spatial patterns and concentrations within datasets.

When to use Hexbin Plot:

• Visualizing the density and distribution of statistics points in two-dimensional area.
• Identifying clusters or concentrations of statistics inside a scatter plot.
• Handling massive datasets with overlapping data factors in a clear and informative way.

15. Violin Plot

A violin plot combines a box plot with a kernel density plot to show the distribution of statistics together with its summary statistics. It is useful for comparing the distribution of more than one organizations or categories. Violin plots provide insights into the shape, unfold, and important tendency of statistics distributions.

When to use Violin Plot:

• Comparing the distribution of continuous variables across distinctive groups or categories.
• Visualizing the shape and spread of information distributions, including skewness and multimodality.
• Presenting precis information and outliers within information distributions in a visually appealing layout.

Visualization Charts for Textual and Symbolic data

Data visualization charts types for textual and symbolic data symbolize facts that is basically composed of words, symbols, or other non-numeric bureaucracy. Some common visualization charts for textual and symbolic facts consist of:

• Word Cloud
• Pictogram Chart

These charts are particularly useful for studying textual facts, identifying key topics or subjects, visualizing keyword frequency, and highlighting enormous phrases or ideas in qualitative analysis or sentiment analysis.

1. Word Cloud

A word cloud is a visual representation of textual content records in which phrases are sized based totally on their frequency or significance inside the textual content. Common words seem larger and greater outstanding, at the same time as less common phrases are smaller. Word clouds provide a short and intuitive manner to identify distinguished phrases or issues within a frame of textual content.

When to use Word Cloud:

• Identifying key themes or subjects within a massive corpus of text.
• Visualizing keyword frequency or distribution in textual facts.
• Highlighting giant terms or principles in qualitative evaluation or sentiment evaluation.

2. Pictogram Chart

A pictogram chart makes use of icons or symbols to represent information values, wherein the size or amount of icons corresponds to the value they represent. It is an powerful way to deliver information in a visually appealing way, mainly when coping with categorical or qualitative records.

When to use pictograph chart:

• Presenting records in a visually enticing format, specially for non-numeric or qualitative records.
• Communicating information to audiences with various tiers of literacy or language talent.
• Emphasizing key statistics points or tendencies the usage of without difficulty recognizable symbols or icons.

Temporal and Trend Charts Data Visualization

Best Data visualization charts for Temporal and trend charts are visualization techniques used to investigate and visualize patterns, traits, and changes over time. These charts are mainly powerful for exploring time-series data, wherein information points are associated with particular timestamps or time periods. Temporal and trend charts provide insights into how statistics evolves over the years and assist perceive recurring styles, anomalies, and tendencies. Some common styles of temporal charts include:

• Line chart
• Streamgraph
• Bullet Graph
• Gantt Chart
• Waterfall Chart

1. Streamgraph

A streamgraph visualizes the trade in the composition of a dataset over time by using stacking regions alongside a baseline. It is useful for displaying trends and styles in temporal data at the same time as preserving continuity throughout time periods. Streamgraphs are especially effective for visualizing sluggish shifts or changes in data distribution over the years.

When to use streamplot:

• Analyzing trends and changes in facts distribution over the years.
• Comparing the relative contributions of different classes or organizations within a dataset.
• Highlighting patterns or fluctuations in facts through the years in a visually attractive manner.

2. Bullet Graph

A bullet graph is a variant of a bar chart designed to expose progress towards a aim or performance towards a target. It includes a single bar supplemented by reference traces and markers to provide context and comparison. Bullet graphs are beneficial for presenting key overall performance signs (KPIs) and monitoring progress toward goals.

When to use Bullet Graph:

• Displaying development toward goals or objectives in a concise and informative manner.
• Comparing real performance in opposition to predefined benchmarks or thresholds.
• Communicating overall performance metrics successfully in dashboards or reports.

3. Gantt Chart

A Gantt chart visualizes challenge schedules or timelines through representing duties or sports as horizontal bars along a time axis. It is beneficial for planning, scheduling, and monitoring progress in venture control. Gantt charts offer a visual evaluation of venture timelines, dependencies, and aid allocation.

When to use Gantt Chart:

• Planning and scheduling complicated tasks with multiple duties and dependencies.
• Tracking progress and managing resources at some stage in the mission lifecycle.
• Communicating undertaking timelines and milestones to stakeholders and team participants.

4. Waterfall Chart

A waterfall chart visualizes the cumulative impact of sequential high-quality and negative values on an preliminary starting point. It is generally utilized in financial analysis to show adjustments in net price over time. Waterfall charts provide a clean visual representation of the way individual factors make contributions to the general alternate in a dataset.

When to use waterfall chart:

• Analyzing and visualizing modifications in economic performance or budget allocations through the years.
• Identifying the sources of gains or losses within a dataset and their cumulative impact.
• Presenting complicated statistics ameliorations or calculations in a clear and concise layout.

Curse of Dimensionality

The Curse of Dimensionality in Machine Learning arises when working with high-dimensional data, leading to increased computational complexity, overfitting, and spurious correlations. 

What is the Curse of Dimensionality?

• The Curse of Dimensionality refers to the phenomenon where the efficiency and effectiveness of algorithms deteriorate as the dimensionality of the data increases exponentially.
• In high-dimensional spaces, data points become sparse, making it challenging to discern meaningful patterns or relationships due to the vast amount of data required to adequately sample the space.
• The Curse of Dimensionality significantly impacts machine learning algorithms in various ways. It leads to increased computational complexity, longer training times, and higher resource requirements. Moreover, it escalates the risk of overfitting and spurious correlations, hindering the algorithms’ ability to generalize well to unseen data.

How to Overcome the Curse of Dimensionality?

To overcome the curse of dimensionality, you can consider the following strategies:

Dimensionality Reduction Techniques:

• Feature Selection: Identify and select the most relevant features from the original dataset while discarding irrelevant or redundant ones. This reduces the dimensionality of the data, simplifying the model and improving its efficiency.
• Feature Extraction: Transform the original high-dimensional data into a lower-dimensional space by creating new features that capture the essential information. Techniques such as Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE) are commonly used for feature extraction.

Data Preprocessing:

• Normalization: Scale the features to a similar range to prevent certain features from dominating others, especially in distance-based algorithms.
• Handling Missing Values: Address missing data appropriately through imputation or deletion to ensure robustness in the model training process.

Python Implementation of Mitigating Curse Of Dimensionality

Here we are using the dataset uci-secom.

Import Necessary Libraries

Import required libraries including scikit-learn modules for dataset loading, model training, data preprocessing, dimensionality reduction, and evaluation.

import numpy as np
import pandas as pd
from sklearn.feature_selection import SelectKBest, f_classif, VarianceThreshold
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.impute import SimpleImputer

Loading the dataset

The Dataset is stored in a CSV file named 'your_dataset.csv', and have a timestamp column named 'Time' and a target variable column named 'Pass/Fail'.

df = pd.read_csv('your_dataset.csv')

# Assuming 'X' contains your features and 'y' contains your target variable
X = df.drop(columns=['Time', 'Pass/Fail'])
y = df['Pass/Fail']

Remove Constant Features

• We are using VarianceThreshold to remove constant features and SimpleImputer to impute missing values with the mean.

# Remove constant features
selector = VarianceThreshold()
X_selected = selector.fit_transform(X)

# Impute missing values
imputer = SimpleImputer(strategy='mean')
X_imputed = imputer.fit_transform(X_selected)

Splitting the data and standardizing

# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X_imputed, y, test_size=0.2, random_state=42)

# Standardize the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Feature Selection and Dimensionality Reduction

1. Feature Selection: SelectKBest is used to select the top k features based on a specified scoring function (f_classif in this case). It selects the features that are most likely to be related to the target variable.
2. Dimensionality Reduction: PCA (Principal Component Analysis) is then used to further reduce the dimensionality of the selected features. It transforms the data into a lower-dimensional space while retaining as much variance as possible.

# Perform feature selection
selector_kbest = SelectKBest(score_func=f_classif, k=20)
X_train_selected = selector_kbest.fit_transform(X_train_scaled, y_train)
X_test_selected = selector_kbest.transform(X_test_scaled)

# Perform dimensionality reduction
pca = PCA(n_components=10)
X_train_pca = pca.fit_transform(X_train_selected)
X_test_pca = pca.transform(X_test_selected)

Training the classifiers

1. Training Before Dimensionality Reduction: Train a Random Forest classifier (clf_before) on the original scaled features (X_train_scaled) without dimensionality reduction.
2. Evaluation Before Dimensionality Reduction: Make predictions (y_pred_before) on the test set (X_test_scaled) using the classifier trained before dimensionality reduction, and calculate the accuracy (accuracy_before) of the model.
3. Training After Dimensionality Reduction: Train a new Random Forest classifier (clf_after) on the reduced feature set (X_train_pca) after dimensionality reduction.
4. Evaluation After Dimensionality Reduction: Make predictions (y_pred_after) on the test set (X_test_pca) using the classifier trained after dimensionality reduction, and calculate the accuracy (accuracy_after) of the model.

# Train a classifier (e.g., Random Forest) without dimensionality reduction
clf_before = RandomForestClassifier(n_estimators=100, random_state=42)
clf_before.fit(X_train_scaled, y_train)

# Make predictions and evaluate the model before dimensionality reduction
y_pred_before = clf_before.predict(X_test_scaled)
accuracy_before = accuracy_score(y_test, y_pred_before)
print(f'Accuracy before dimensionality reduction: {accuracy_before}')
# Train a classifier (e.g., Random Forest) on the reduced feature set
clf_after = RandomForestClassifier(n_estimators=100, random_state=42)
clf_after.fit(X_train_pca, y_train)

# Make predictions and evaluate the model after dimensionality reduction
y_pred_after = clf_after.predict(X_test_pca)
accuracy_after = accuracy_score(y_test, y_pred_after)
print(f'Accuracy after dimensionality reduction: {accuracy_after}')

OUTPUT:
Accuracy before dimensionality reduction: 0.8745
Accuracy after dimensionality reduction: 0.9235668789808917

The accuracy before dimensionality reduction is 0.8745, while the accuracy after dimensionality reduction is 0.9236. This improvement indicates that the dimensionality reduction technique (PCA in this case) helped the model generalize better to unseen data.

Correlation Analysis

Correlation analysis is a statistical technique for determining the strength of a link between two variables. It is used to detect patterns and trends in data and to forecast future occurrences.

• Consider a problem with different factors to be considered for making optimal conclusions
• Correlation explains how these variables are dependent on each other.
• Correlation quantifies how strong the relationship between two variables is. A higher value of the correlation coefficient implies a stronger association.
• The sign of the correlation coefficient indicates the direction of the relationship between variables. It can be either positive, negative, or zero.

What is Correlation?

The Pearson correlation coefficient is the most often used metric of correlation. It expresses the linear relationship between two variables in numerical terms. The Pearson correlation coefficient, written as “r,” is as follows:

                                                        r=∑(xi​−xˉ)2∑(yi​−yˉ​)2​∑(xi​−xˉ)(yi​−yˉ​)​

$r=\frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum (x_i-\bar{x}{)}^2\sum (y_i-\bar{y}{)}^2}}$

where,

• r: Correlation coefficient 
• $x_i$ : ith value first dataset X
• $\bar{x}$ : Mean of first dataset X
• $y_i$ : ith value second dataset Y
• $\bar{y}$ : Mean of second dataset Y

The correlation coefficient, denoted by “r”, ranges between -1 and 1.

r = -1 indicates a perfect negative correlation.
r = 0 indicates no linear correlation between the variables.
r = 1 indicates a perfect positive correlation.

Types of Correlation

There are three types of correlation:

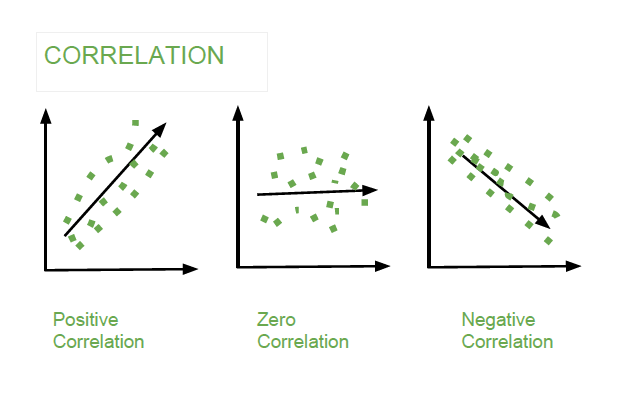
1. Positive Correlation: Positive correlation indicates that two variables have a direct relationship. As one variable increases, the other variable also increases. For example, there is a positive correlation between height and weight. As people get taller, they also tend to weigh more.
2. Negative Correlation: Negative correlation indicates that two variables have an inverse relationship. As one variable increases, the other variable decreases. For example, there is a negative correlation between price and demand. As the price of a product increases, the demand for that product decreases.
3. Zero Correlation: Zero correlation indicates that there is no relationship between two variables. The changes in one variable do not affect the other variable. For example, there is zero correlation between shoe size and intelligence.

A positive correlation indicates that the two variables move in the same direction, while a negative correlation indicates that the two variables move in opposite directions.

The strength of the correlation is measured by a correlation coefficient, which can range from -1 to 1. A correlation coefficient of 0 indicates no correlation, while a correlation coefficient of 1 or -1 indicates a perfect correlation.

Correlation Coefficients

The different types of correlation coefficients used to measure the relation between two variables are:

Correlation Coefficient	Type of Relation	Levels of Measurement	Data Distribution
Pearson Correlation Coefficient	Linear	Interval/Ratio	Normal distribution
Spearman Rank Correlation Coefficient	Non-Linear	Ordinal	Any distribution
Kendall Tau Coefficient	Non-Linear	Ordinal	Any distribution
Phi Coefficient	Non-Linear	Nominal vs. Nominal (nominal with 2 categories (dichotomous))	Any distribution
Cramer’s V	Non-Linear	Two nominal variables	Any distribution

How to Conduct Correlation Analysis

To conduct a correlation analysis, you will need to follow these steps:

1. Identify Variable: Identify the two variables that we want to correlate. The variables should be quantitative, meaning that they can be represented by numbers.
2. Collect data : Collect data on the two variables. We can collect data from a variety of sources, such as surveys, experiments, or existing records.
3. Choose the appropriate correlation coefficient. The Pearson correlation coefficient is the most commonly used correlation coefficient, but there are other correlation coefficients that may be more appropriate for certain types of data.
4. Calculate the correlation coefficient. We can use a statistical software package to calculate the correlation coefficient, or you can use a formula.
5. Interpret the correlation coefficient. The correlation coefficient can be interpreted as a measure of the strength and direction of the linear relationship between the two variables.

Implementations

Python provides libraries such as “NumPy” and “Pandas” which have various methods to ease various calculations, including correlation analysis.

Using NumPy

import numpy as np

# Create sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 7, 3, 9, 1])

# Calculate correlation coefficient
correlation_coefficient = np.corrcoef(x, y)

print("Correlation Coefficient:", correlation_coefficient)

Output:

Correlation Coefficient: [[ 1.  -0.3]
 [-0.3  1. ]]

Using pandas

import pandas as pd

# Create a DataFrame with sample data
data = pd.DataFrame({'X': [1, 2, 3, 4, 5], 'Y': [5, 7, 3, 9, 1]})

# Calculate correlation coefficient
correlation_coefficient = data['X'].corr(data['Y'])

print("Correlation Coefficient:", correlation_coefficient)

Output:

Correlation Coefficient: -0.3

Interpretation of Correlation coefficients

• Perfect: 0.80 to 1.00
• Strong: 0.50 to 0.79
• Moderate: 0.30 to 0.49
• Weak: 0.00 to 0.29

Value greater than 0.7 is considered a strong correlation between variables.

Applications of Correlation Analysis

Correlation Analysis is an important tool that helps in better decision-making, enhances predictions and enables better optimization techniques across different fields. Predictions or decision making dwell on the relation between the different variables to produce better results, which can be achieved by correlation analysis.

The various fields in which it can be used are:

• Economics and Finance : Help in analyzing the economic trends by understanding the relations between supply and demand.
• Business Analytics : Helps in making better decisions for the company and provides valuable insights.
• Market Research and Promotions : Helps in creating better marketing strategies by analyzing the relation between recent market trends and customer behavior.
• Medical Research : Correlation can be employed in Healthcare so as to better understand the relation between different symptoms of diseases and understand genetical diseases better.
• Weather Forecasts: Analyzing the correlation between different variables so as to predict weather.
• Better Customer Service : Helps in better understand the customers and significantly increases the quality of customer service.
• Environmental Analysis: help create better environmental policies by understanding various environmental factors.

Advantages of Correlation Analysis

• Correlation analysis helps us understand how two variables affect each other or are related to each other.
• They are simple and very easy to interpret.
• Aids in decision-making process in business, healthcare, marketing, etc
• Helps in feature selection in machine learning.
• Gives a measure of the relation between two variables.

Disadvantages of Correlation Analysis

• Correlation does not imply causation, which means a variable may not be the cause for the other variable even though they are correlated.
• If outliers are not dealt with well they may cause errors.
• It works well only on bivariate relations and may not produce accurate results for multivariate relations.
• Complex relations can not be analyzed accurately.

Principal Component Analysis

Principal Component Analysis is an unsupervised learning algorithm that is used for the dimensionality reduction in machine learning. It is a statistical process that converts the observations of correlated features into a set of linearly uncorrelated features with the help of orthogonal transformation. These new transformed features are called the Principal Components. It is one of the popular tools that is used for exploratory data analysis and predictive modeling. It is a technique to draw strong patterns from the given dataset by reducing the variances.

PCA generally tries to find the lower-dimensional surface to project the high-dimensional data.

PCA works by considering the variance of each attribute because the high attribute shows the good split between the classes, and hence it reduces the dimensionality. Some real-world applications of PCA are image processing, movie recommendation system, optimizing the power allocation in various communication channels. It is a feature extraction technique, so it contains the important variables and drops the least important variable.

The PCA algorithm is based on some mathematical concepts such as:

• Variance and Covariance
• Eigenvalues and Eigen factors

Some common terms used in PCA algorithm:

• Dimensionality: It is the number of features or variables present in the given dataset. More easily, it is the number of columns present in the dataset.
• Correlation: It signifies that how strongly two variables are related to each other. Such as if one changes, the other variable also gets changed. The correlation value ranges from -1 to +1. Here, -1 occurs if variables are inversely proportional to each other, and +1 indicates that variables are directly proportional to each other.
• Orthogonal: It defines that variables are not correlated to each other, and hence the correlation between the pair of variables is zero.
• Eigenvectors: If there is a square matrix M, and a non-zero vector v is given. Then v will be eigenvector if Av is the scalar multiple of v.
• Covariance Matrix: A matrix containing the covariance between the pair of variables is called the Covariance Matrix.

Principal Components in PCA

As described above, the transformed new features or the output of PCA are the Principal Components. The number of these PCs are either equal to or less than the original features present in the dataset. Some properties of these principal components are given below:

• The principal component must be the linear combination of the original features.
• These components are orthogonal, i.e., the correlation between a pair of variables is zero.
• The importance of each component decreases when going to 1 to n, it means the 1 PC has the most importance, and n PC will have the least importance.

Steps for PCA algorithm

1. Getting the dataset
   Firstly, we need to take the input dataset and divide it into two subparts X and Y, where X is the training set, and Y is the validation set.
2. Representing data into a structure
   Now we will represent our dataset into a structure. Such as we will represent the two-dimensional matrix of independent variable X. Here each row corresponds to the data items, and the column corresponds to the Features. The number of columns is the dimensions of the dataset.
3. Standardizing the data
   In this step, we will standardize our dataset. Such as in a particular column, the features with high variance are more important compared to the features with lower variance.
   If the importance of features is independent of the variance of the feature, then we will divide each data item in a column with the standard deviation of the column. Here we will name the matrix as Z.
4. Calculating the Covariance of Z
   To calculate the covariance of Z, we will take the matrix Z, and will transpose it. After transpose, we will multiply it by Z. The output matrix will be the Covariance matrix of Z.
5. Calculating the Eigen Values and Eigen Vectors
   Now we need to calculate the eigenvalues and eigenvectors for the resultant covariance matrix Z. Eigenvectors or the covariance matrix are the directions of the axes with high information. And the coefficients of these eigenvectors are defined as the eigenvalues.
6. Sorting the Eigen Vectors
   In this step, we will take all the eigenvalues and will sort them in decreasing order, which means from largest to smallest. And simultaneously sort the eigenvectors accordingly in matrix P of eigenvalues. The resultant matrix will be named as P*.
7. Calculating the new features Or Principal Components
   Here we will calculate the new features. To do this, we will multiply the P* matrix to the Z. In the resultant matrix Z*, each observation is the linear combination of original features. Each column of the Z* matrix is independent of each other.
8. Remove less or unimportant features from the new dataset.
   The new feature set has occurred, so we will decide here what to keep and what to remove. It means, we will only keep the relevant or important features in the new dataset, and unimportant features will be removed out.

Applications of Principal Component Analysis

• PCA is mainly used as the dimensionality reduction technique in various AI applications such as computer vision, image compression, etc.
• It can also be used for finding hidden patterns if data has high dimensions. Some fields where PCA is used are Finance, data mining, Psychology, etc.

Principal Component Regression (PCR)

Principal Component Regression (PCR) is a statistical technique for regression analysis that is used to reduce the dimensionality of a dataset by projecting it onto a lower-dimensional subspace. This is done by finding a set of orthogonal (i.e., uncorrelated) linear combinations of the original variables, called principal components, that capture the most variance in the data. The principal components are used as predictors in the regression model, instead of the original variables.

PCR is often used as an alternative to multiple linear regression, especially when the number of variables is large or when the variables are correlated. By using PCR, we can reduce the number of variables in the model and improve the interpretability and stability of the regression results.

Features of the Principal Component Regression (PCR)

Here are some key features of Principal Component Regression (PCR):

• PCR reduces the dimensionality of a dataset by projecting it onto a lower-dimensional subspace, using a set of orthogonal linear combinations of the original variables called principal components.
• PCR is often used as an alternative to multiple linear regression, especially when the number of variables is large or when the variables are correlated.
• By using PCR, we can reduce the number of variables in the model and improve the interpretability and stability of the regression results.
• To perform PCR, we first need to standardize the original variables and then compute the principal components using singular value decomposition (SVD) or eigendecomposition of the covariance matrix of the standardized data.
• The principal components are then used as predictors in a linear regression model, whose coefficients can be estimated using least squares regression or maximum likelihood estimation.

Breaking down the Math behind Principal Component Regression (PCR)

Here is a brief overview of the mathematical concepts underlying Principal Component Regression (PCR):

• Dimensionality reduction: PCR reduces the dimensionality of a dataset by projecting it onto a lower-dimensional subspace, using a set of orthogonal linear combinations of the original variables called principal components. This is a way of summarizing the data by capturing the most important patterns and relationships in the data while ignoring noise and irrelevant information.
• Principal components: The principal components of a dataset are the orthogonal linear combinations of the original variables that capture the most variance in the data. They are obtained by performing singular value decomposition (SVD) or eigendecomposition of the covariance matrix of the standardized data. The number of principal components is typically chosen to be the number of variables, but it can be reduced if there is a large amount of collinearity among the variables.
• Linear regression: PCR uses the principal components as predictors in a linear regression model, whose coefficients can be estimated using least squares regression or maximum likelihood estimation. The fitted model can then be used to make predictions on new data.

Overall, PCR uses mathematical concepts from linear algebra and statistics to reduce the dimensionality of a dataset and improve the interpretability and stability of regression results.

Limitations of Principal Component Regression (PCR)

While Principal Component Regression (PCR) has many advantages, it also has some limitations that should be considered when deciding whether to use it for a particular regression analysis:

• PCR only works well with linear relationships: PCR assumes that the relationship between the predictors and the response variable is linear. If the relationship is non-linear, PCR may not be able to accurately capture it, leading to biased or inaccurate predictions. In such cases, non-linear regression methods may be more appropriate.
• PCR does not handle outliers well: PCR is sensitive to outliers in the data, which can have a disproportionate impact on the principal components and the fitted regression model. Therefore, it is important to identify and handle outliers in the data before applying PCR.
• PCR may not be interpretable: PCR involves a complex mathematical procedure that generates a set of orthogonal linear combinations of the original variables. These linear combinations may not be easily interpretable, especially if the number of variables is large. In contrast, multiple linear regression is more interpretable, since it uses the original variables directly as predictors.
• PCR may not be efficient: PCR is computationally intensive, especially when the number of variables is large. Therefore, it may not be the most efficient method for regression analysis, especially when the dataset is large. In such cases, faster and more efficient regression methods may be more appropriate.

Overall, while PCR has many advantages, it is important to carefully consider its limitations and potential drawbacks before using it for regression analysis.

How Principal Component Regression (PCR) is compared to other regression analysis techniques?

Principal Component Regression (PCR) is often compared to other regression analysis techniques, such as multiple linear regression, principal component analysis (PCA), and partial least squares regression (PLSR). Here are some key differences between PCR and these other techniques:

• PCR vs. multiple linear regression: PCR is similar to multiple linear regression, in that both techniques use linear regression to model the relationship between a set of predictors and a response variable. However, PCR differs from multiple linear regression in that it reduces the dimensionality of the data by projecting it onto a lower-dimensional subspace using the principal components. This can improve the interpretability and stability of the regression results, especially when the number of variables is large or when the variables are correlated.
• PCR vs. PCA: PCR is similar to PCA, in that both techniques use principal components to reduce the dimensionality of the data. However, PCR differs from PCA in that it uses the principal components as predictors in a linear regression model, whereas PCA is an unsupervised technique that only analyzes the structure of the data itself, without using a response variable.
• PCR vs. PLSR: PCR is similar to PLSR, in that both techniques use principal components to reduce the dimensionality of the data and improve the interpretability and stability of the regression results. However, PCR differs from PLSR in that it uses the principal components as predictors in a linear regression model, whereas PLSR uses a weighted combination of the original variables as predictors in a partial least squares regression model. This allows PLSR to better capture non-linear relationships between the predictors and the response variable.

Overall, PCR is a useful technique for regression analysis that can be compared to multiple linear regression, PCA, and PLSR, depending on the specific characteristics of the data and the goals of the analysis.

CART (Classification And Regression Tree) in Machine Learning

CART( Classification And Regression Trees) is a  variation of the decision tree algorithm. It can handle both classification and regression tasks. Scikit-Learn uses the Classification And Regression Tree (CART) algorithm to train  Decision Trees (also called “growing” trees). CART was first produced by Leo Breiman, Jerome Friedman, Richard Olshen, and Charles Stone in 1984.

CART(Classification And Regression Tree) for Decision Tree

CART is a predictive algorithm used in Machine learning and it explains how the target variable’s values can be predicted based on other matters. It is a decision tree where each fork is split into a predictor variable and each node has a prediction for the target variable at the end.

The term CART serves as a generic term for the following categories of decision trees:

• Classification Trees: The tree is used to determine which “class” the target variable is most likely to fall into when it is continuous.
• Regression trees: These are used to predict a continuous variable’s value.

In the decision tree, nodes are split into sub-nodes based on a threshold value of an attribute. The root node is taken as the training set and is split into two by considering the best attribute and threshold value. Further, the subsets are also split using the same logic. This continues till the last pure sub-set is found in the tree or the maximum number of leaves possible in that growing tree.

CART Algorithm

Classification and Regression Trees (CART) is a decision tree algorithm that is used for both classification and regression tasks. It is a supervised learning algorithm that learns from labelled data to predict unseen data.

• Tree structure: CART builds a tree-like structure consisting of nodes and branches. The nodes represent different decision points, and the branches represent the possible outcomes of those decisions. The leaf nodes in the tree contain a predicted class label or value for the target variable.
• Splitting criteria: CART uses a greedy approach to split the data at each node. It evaluates all possible splits and selects the one that best reduces the impurity of the resulting subsets. For classification tasks, CART uses Gini impurity as the splitting criterion. The lower the Gini impurity, the more pure the subset is. For regression tasks, CART uses residual reduction as the splitting criterion. The lower the residual reduction, the better the fit of the model to the data.
• Pruning: To prevent overfitting of the data, pruning is a technique used to remove the nodes that contribute little to the model accuracy. Cost complexity pruning and information gain pruning are two popular pruning techniques. Cost complexity pruning involves calculating the cost of each node and removing nodes that have a negative cost. Information gain pruning involves calculating the information gain of each node and removing nodes that have a low information gain.

How does CART algorithm works?

The CART algorithm works via the following process:

• The best-split point of each input is obtained. 
• Based on the best-split points of each input in Step 1, the new “best” split point is identified. 
• Split the chosen input according to the “best” split point. 
• Continue splitting until a stopping rule is satisfied or no further desirable splitting is available.

CART algorithm uses Gini Impurity to split the dataset into a decision tree .It does that by searching for the best homogeneity for the sub nodes, with the help of the Gini index criterion.

Gini index/Gini impurity

The Gini index is a metric for the classification tasks in CART. It stores the sum of squared probabilities of each class. It computes the degree of probability of a specific variable that is wrongly being classified when chosen randomly and a variation of the Gini coefficient. It works on categorical variables, provides outcomes either “successful” or “failure” and hence conducts binary splitting only.

The degree of the  Gini index varies from 0 to 1,

• Where 0 depicts that all the elements are allied to a certain class, or only one class exists there.
• The Gini index of value 1 signifies that all the elements are randomly distributed across various classes, and
• A value of 0.5 denotes the elements are uniformly distributed into some classes.

Mathematically, we can write Gini Impurity as follows: 

where Pi is the probability of an object being classified to a particular class.

CART for Classification

A classification tree is an algorithm where the target variable is categorical. The algorithm is then used to identify the “Class” within which the target variable is most likely to fall. Classification trees are used when the dataset needs to be split into classes that belong to the response variable(like yes or no)

For classification in decision tree learning algorithm that creates a tree-like structure to predict class labels. The tree consists of nodes, which represent different decision points, and branches, which represent the possible result of those decisions. Predicted class labels are present at each leaf node of the tree.

How Does CART for Classification Work?

CART for classification works by recursively splitting the training data into smaller and smaller subsets based on certain criteria. The goal is to split the data in a way that minimizes the impurity within each subset. Impurity is a measure of how mixed up the data is in a particular subset. For classification tasks, CART uses Gini impurity

• Gini Impurity- Gini impurity measures the probability of misclassifying a random instance from a subset labeled according to the majority class. Lower Gini impurity means more purity of the subset.
• Splitting Criteria- The CART algorithm evaluates all potential splits at every node and chooses the one that best decreases the Gini impurity of the resultant subsets. This process continues until a stopping criterion is reached, like a maximum tree depth or a minimum number of instances in a leaf node.

CART for Regression

A Regression tree is an algorithm where the target variable is continuous and the tree is used to predict its value. Regression trees are used when the response variable is continuous. For example, if the response variable is the temperature of the day.

CART for regression is a decision tree learning method that creates a tree-like structure to predict continuous target variables. The tree consists of nodes that represent different decision points and branches that represent the possible outcomes of those decisions. Predicted values for the target variable are stored in each leaf node of the tree.

How Does CART works for Regression?

Regression CART works by splitting the training data recursively into smaller subsets based on specific criteria. The objective is to split the data in a way that minimizes the residual reduction in each subset.

• Residual Reduction- Residual reduction is a measure of how much the average squared difference between the predicted values and the actual values for the target variable is reduced by splitting the subset. The lower the residual reduction, the better the model fits the data.
• Splitting Criteria- CART evaluates every possible split at each node and selects the one that results in the greatest reduction of residual error in the resulting subsets. This process is repeated until a stopping criterion is met, such as reaching the maximum tree depth or having too few instances in a leaf node.

Pseudo-code of the CART algorithm

d = 0, endtree = 0
Note(0) = 1, Node(1) = 0, Node(2) = 0
while endtree < 1
    if Node(2d-1) + Node(2d) + .... + Node(2d+1-2) = 2 - 2d+1   
        endtree = 1
    else
        do i = 2d-1, 2d, .... , 2d+1-2
            if Node(i) > -1
                Split tree
            else 
                Node(2i+1) = -1
                Node(2i+2) = -1
            end if
        end do
    end if
d = d + 1
end while

CART model representation

CART models are formed by picking input variables and evaluating split points on those variables until an appropriate tree is produced.

Steps to create a Decision Tree using the  CART algorithm:

• Greedy algorithm: In this The input space is divided using the  Greedy method which is known as a recursive binary spitting.  This is a numerical method within which all of the values are aligned and several other split points are tried and assessed using a cost function.
• Stopping Criterion: As it works its way down the tree with the training data, the recursive binary splitting method described above must know when to stop splitting. The most frequent halting method is to utilize a minimum amount of training data allocated to every leaf node. If the count is smaller than the specified threshold, the split is rejected and also the node is considered the last leaf node.
• Tree pruning: Decision tree’s complexity is defined as the number of splits in the tree. Trees with fewer branches are recommended as they are simple to grasp and less prone to cluster the data. Working through each leaf node in the tree and evaluating the effect of deleting it using a hold-out test set is the quickest and simplest pruning approach.
• Data preparation for the  CART:  No special data preparation is required for the CART algorithm.

Decision Tree CART Implementations

Here is the code implements the CART algorithm for classifying fruits based on their color and size. It first encodes the categorical data using a LabelEncoder and then trains a CART classifier on the encoded data. Finally, it predicts the fruit type for a new instance and decodes the result back to its original categorical value.

from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import LabelEncoder

# Define the features and target variable
features = [
    ["red", "large"],
    ["green", "small"],
    ["red", "small"],
    ["yellow", "large"],
    ["green", "large"],
    ["orange", "large"],
]
target_variable = ["apple", "lime", "strawberry", "banana", "grape", "orange"]

# Flatten the features list for encoding
flattened_features = [item for sublist in features for item in sublist]

# Use a single LabelEncoder for all features and target variable
le = LabelEncoder()
le.fit(flattened_features + target_variable)

# Encode features and target variable
encoded_features = [le.transform(item) for item in features]
encoded_target = le.transform(target_variable)

# Create a CART classifier
clf = DecisionTreeClassifier()

# Train the classifier on the training set
clf.fit(encoded_features, encoded_target)

# Predict the fruit type for a new instance
new_instance = ["red", "large"]
encoded_new_instance = le.transform(new_instance)
predicted_fruit_type = clf.predict([encoded_new_instance])
decoded_predicted_fruit_type = le.inverse_transform(predicted_fruit_type)
print("Predicted fruit type:", decoded_predicted_fruit_type[0])

Output:

Predicted fruit type: apple

POPULAR CART-BASED ALGORITHMS:

• CART (Classification and Regression Trees): The original algorithm that uses binary splits to build decision trees.
• C4.5 and C5.0: Extensions of CART that allow for multiway splits and handle categorical variables more effectively.
• Random Forests: Ensemble methods that use multiple decision trees (often CART) to improve predictive performance and reduce overfitting.
• Gradient Boosting Machines (GBM): Boosting algorithms that also use decision trees (often CART) as base learners, sequentially improving model performance.

Advantages of CART

• Results are simplistic.
• Classification and regression trees are Nonparametric and Nonlinear.
• Classification and regression trees implicitly perform feature selection.
• Outliers have no meaningful effect on CART.
• It requires minimal supervision and produces easy-to-understand models.

Limitations of CART

• Overfitting.
• High Variance.
• low bias.
• the tree structure may be unstable.

Applications of the CART algorithm

• For quick Data insights.
• In Blood Donors Classification.
• For environmental and ecological data.
• In the financial sectors.

Module 3

Performance Evaluation

Evaluation Metrics in Machine Learning

Classification Metrics

In a classification task, the main task is to predict the target variable which is in the form of discrete values. To evaluate the performance of such a model there are metrics as mentioned below:

• Classification Accuracy
• Logarithmic loss
• Area under Curve
• F1 score
  • Precision
  • Recall
• Confusion Matrix

Regression Evaluation Metrics

In the regression task, the work is to predict the target variable which is in the form of continuous values. To evaluate the performance of such a model below mentioned evaluation metrics are used:

• Mean Absolute Error
• Mean Squared Error
• Root Mean Square Error
• Root Mean Square Logarithmic Error
• R2 – Score

Techniques To Evaluate Accuracy of Classifier in Data Mining

HoldOut

In the holdout method, the largest dataset is randomly divided into three subsets:

• A training set is a subset of the dataset which are been used to build predictive models.
• The validation set is a subset of the dataset which is been used to assess the performance of the model built in the training phase. It provides a test platform for fine-tuning of the model’s parameters and selecting the best-performing model. It is not necessary for all modeling algorithms to need a validation set.
• Test sets or unseen examples are the subset of the dataset to assess the likely future performance of the model. If a model is fitting into the training set much better than it fits into the test set, then overfitting is probably the cause that occurred here.

Basically, two-thirds of the data are been allocated to the training set and the remaining one-third is been allocated to the test set.

Random Subsampling

• Random subsampling is a variation of the holdout method. The holdout method is been repeated K times.
• The holdout subsampling involves randomly splitting the data into a training set and a test set.
• On the training set the data is been trained and the mean square error (MSE) is been obtained from the predictions on the test set.
• As MSE is dependent on the split, this method is not recommended. So a new split can give you a new MSE.
• The overall accuracy is been calculated as 

E=1/k ∑ (i= 1 to k) Eᵢ

Cross-Validation

• K-fold cross-validation is been used when there is only a limited amount of data available, to achieve an unbiased estimation of the performance of the model.
• Here, we divide the data into K subsets of equal sizes.
• We build models K times, each time leaving out one of the subsets from the training, and use it as the test set.
• If K equals the sample size, then this is called a “Leave-One-Out”

Bootstrapping

• Bootstrapping is one of the techniques which is used to make the estimations from the data by taking an average of the estimates from smaller data samples.
• The bootstrapping method involves the iterative resampling of a dataset with replacement.
• On resampling instead of only estimating the statistics once on complete data, we can do it many times.
• Repeating this multiple times helps to obtain a vector of estimates.
• Bootstrapping can compute variance, expected value, and other relevant statistics of these estimates.

Log Loss

It is the evaluation measure to check the performance of the classification model. It measures the amount of divergence of predicted probability with the actual label. So lesser the log loss value, more the perfectness of model. For a perfect model, log loss value = 0. For instance, as accuracy is the count of correct predictions i.e. the prediction that matches the actual label, Log Loss value is the measure of uncertainty of our predicted labels based on how it varies from the actual label.

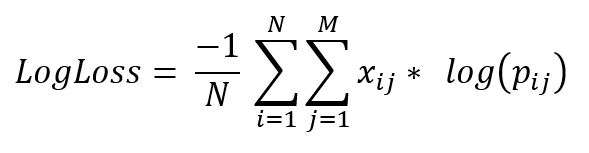
where, 
N  : no. of samples.
M  : no. of attributes.
xij : indicates whether ith sample belongs to jth class or not.
pij : indicates probability of ith sample belonging to jth class.

Implementation of logloss using sklearn

    from sklearn.metrics import log_loss

    LogLoss = log_loss(y_true, y_pred, eps = 1e-15, normalize = True, sample_weight = None, labels = None)

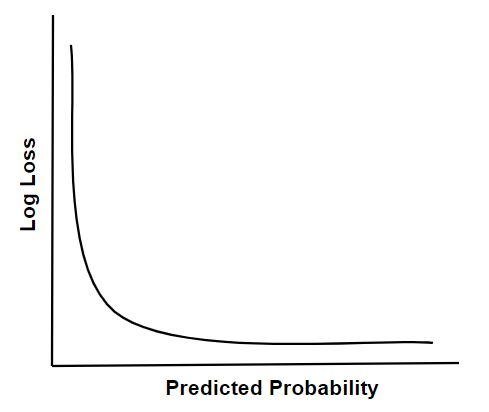
Mean Squared Error

It is simply the average of the square of the difference between the original values and the predicted values.

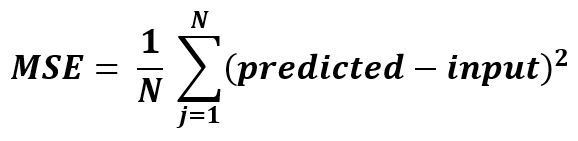
Implementation of Mean Squared Error using sklearn

from sklearn.metrics import mean_squared_error

MSE = mean_squared_error(y_true, y_pred)

AUC ROC Curve in Machine Learning

The AUC-ROC curve, or Area Under the Receiver Operating Characteristic curve, is a graphical representation of the performance of a binary classification model at various classification thresholds. It is commonly used in machine learning to assess the ability of a model to distinguish between two classes, typically the positive class (e.g., presence of a disease) and the negative class (e.g., absence of a disease).

Receiver Operating Characteristics (ROC) Curve:

ROC stands for Receiver Operating Characteristics, and the ROC curve is the graphical representation of the effectiveness of the binary classification model. It plots the true positive rate (TPR) vs the false positive rate (FPR) at different classification thresholds.

Area Under Curve (AUC) Curve:

AUC stands for the Area Under the Curve, and the AUC curve represents the area under the ROC curve. It measures the overall performance of the binary classification model. As both TPR and FPR range between 0 to 1, So, the area will always lie between 0 and 1, and A greater value of AUC denotes better model performance. Our main goal is to maximize this area in order to have the highest TPR and lowest FPR at the given threshold. The AUC measures the probability that the model will assign a randomly chosen positive instance a higher predicted probability compared to a randomly chosen negative instance.

 It represents the probability with which our model can distinguish between the two classes present in our target. 

ROC-AUC Classification Evaluation Metric

How does AUC-ROC work?

An AUC of 0.75 would actually mean that let’s say we take two data points belonging to separate classes then there is a 75% chance the model would be able to segregate them or rank order them correctly i.e positive point has a higher prediction probability than the negative class. (assuming a higher prediction probability means the point would ideally belong to the positive class). Here is a small example to make things more clear.

Index	Class	Probability
P1	1	0.95
P2	1	0.90
P3	0	0.85
P4	0	0.81
P5	1	0.78
P6	0	0.70

Here we have 6 points where P1, P2, and P5 belong to class 1 and P3, P4, and P6 belong to class 0 and we’re corresponding predicted probabilities in the Probability column, as we said if we take two points belonging to separate classes then what is the probability that model rank orders them correctly.

We will take all possible pairs such that one point belongs to class 1 and the other belongs to class 0, we will have a total of 9 such pairs below are all of these 9 possible pairs.

Pair	isCorrect
(P1,P3)	Yes
(P1,P4)	Yes
(P1,P6)	Yes
(P2,P3)	Yes
(P2,P4)	Yes
(P2,P6)	Yes
(P3,P5)	No
(P4,P5)	No
(P5,P6)	Yes

Here column isCorrect tells if the mentioned pair is correctly rank-ordered based on the predicted probability i.e class 1 point has a higher probability than class 0 point, in 7 out of these 9 possible pairs class 1 is ranked higher than class 0, or we can say that there is a 77% chance that if you pick a pair of points belonging to separate classes the model would be able to distinguish them correctly.

Confusion matrix

A confusion matrix is a matrix that summarizes the performance of a machine learning model on a set of test data. It is a means of displaying the number of accurate and inaccurate instances based on the model’s predictions. It is often used to measure the performance of classification models, which aim to predict a categorical label for each input instance.

The matrix displays the number of instances produced by the model on the test data.

True Positive (TP): The model correctly predicted a positive outcome (the actual outcome was positive).

True Negative (TN): The model correctly predicted a negative outcome (the actual outcome was negative).

False Positive (FP): The model incorrectly predicted a positive outcome (the actual outcome was negative). Also known as a Type I error.

False Negative (FN): The model incorrectly predicted a negative outcome (the actual outcome was positive). Also known as a Type II error.

Metrics based on Confusion Matrix Data

1. Accuracy

Accuracy is used to measure the performance of the model. It is the ratio of Total correct instances to the total instances. 

$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$

2. Precision

Precision is a measure of how accurate a model’s positive predictions are. It is defined as the ratio of true positive predictions to the total number of positive predictions made by the model.

$\text{Precision}=\frac{TP}{TP+FP}$

3. Recall

Recall measures the effectiveness of a classification model in identifying all relevant instances from a dataset. It is the ratio of the number of true positive (TP) instances to the sum of true positive and false negative (FN) instances.

$\text{Recall}=\frac{TP}{TP+FN}$

4. F1-Score

F1-score is used to evaluate the overall performance of a classification model. It is the harmonic mean of precision and recall,

$\text{F1-Score}=\frac{2\cdot Precision\cdot Recall}{Precision+Recall}$

5. Specificity

Specificity is another important metric in the evaluation of classification models, particularly in binary classification. It measures the ability of a model to correctly identify negative instances. Specificity is also known as the True Negative Rate. Formula is given by:

$\text{Specificity}=\frac{TN}{TN+FP}$

6. Type 1 and Type 2 error

1. Type 1 error

Type 1 error occurs when the model predicts a positive instance, but it is actually negative. Precision is affected by false positives, as it is the ratio of true positives to the sum of true positives and false positives.

$\text{Type 1 Error}=\frac{FP}{TN+FP}$

2. Type 2 error

Type 2 error occurs when the model fails to predict a positive instance. Recall is directly affected by false negatives, as it is the ratio of true positives to the sum of true positives and false negatives.

$=\frac{FN}{TP+FN}$

Precision emphasizes minimizing false positives, while recall focuses on minimizing false negatives.

Mean Absolute Error:

• Mean Absolute Error calculates the average difference between the calculated values and actual values. 
• Also known as scale-dependent accuracy.
• used as evaluation metrics for regression models in machine learning.

Mean Absolute Error = (1/n) * ∑|yi – xi|

where,

yi: Actual value

xi: Calculated value

n: Total number of observations

Mean Squared Error : 

The Mean Squared Error (MSE) or Mean Squared Deviation (MSD) of an estimator measures the average of error squares i.e. the average squared difference between the estimated values and true value. It is a risk function, corresponding to the expected value of the squared error loss. It is always non – negative and values close to zero are better. The MSE is the second moment of the error (about the origin) and thus incorporates both the variance of the estimator and its bias. 

Steps to find the MSE

1. Find the equation for the regression line.

   (1) 

2. Insert X values in the equation found in step 1 in order to get the respective Y values i.e.

   (2) 

3. Now subtract the new Y values from the original Y values. Thus, found values are the error terms. It is also known as the vertical distance of the given point from the regression line.

   (3) 

4. Square the errors found in step 3.

   (4) 

5. Sum up all the squares.

   (5) 

6. Divide the value found in step 5 by the total number of observations.

                                                                                                       (6)

Root mean squared error (RMSE):

• RMSE is the square root of the MSE. 
• RMSE is the average distance between the predicted and actual values, while MSE is the average squared difference between the two. 
• MSE is often used to train a regression prediction model, while RMSE is used to evaluate and report its performance.

The formula for calculating RMSE is sqrt(MSE)

Root Mean Squared Logarithmic Error(RMSLE)

There are times when the target variable varies in a wide range of values. And hence we do not want to penalize the overestimation of the target values but penalize the underestimation of the target values. For such cases, RMSLE is used as an evaluation metric which helps us to achieve the above objective.

The formulae is:

            RMSLE=N∑j=1N​(log(y^​j​+1)–log(yj​+1))2​​
Over

Oversampling:

Synthetic Minority Over-Sampling Technique

The Synthetic Minority Over-Sampling Technique (SMOTE) is a powerful method used to handle class imbalance in datasets. SMOTE handles this issue by generating samples of minority classes to make the class distribution balanced. SMOTE works by generating synthetic examples in the feature space of the minority class.

Working Procedure of SMOTE

1. Identify Minority Class Instances: SMOTE operates on datasets where one or more classes are significantly underrepresented compared to others. The first step is to identify the minority class or classes in the dataset.
2. Nearest Neighbor Selection: For each minority class instance, SMOTE identifies its k nearest neighbors in the feature space. The number of nearest neighbors, denoted as k, is a parameter specified by the user.
3. Synthetic Sample Generation: For each minority class instance, SMOTE randomly selects one of its k nearest neighbors. It then generates synthetic samples along the line segment joining the minority class instance and the selected nearest neighbor in the feature space.
4. Controlled Oversampling: The amount of oversampling is controlled by a parameter called the oversampling ratio, which specifies the desired ratio of synthetic samples to real minority class samples. By default, SMOTE typically aims to balance the class distribution by generating synthetic samples until the minority class reaches the same size as the majority class.
5. Repeat for All Minority Class Instances: Steps 2-4 are repeated for all minority class instances in the dataset, generating synthetic samples to augment the minority class.
6. Create Balanced Dataset: After generating synthetic samples for the minority class, the resulting dataset becomes more balanced, with a more equitable distribution of instances across classes.

Module 4

Multiple Linear Regression:

What is Linear Regression?

Linear regression is a type of supervised machine learning algorithm that computes the linear relationship between the dependent variable and one or more independent features by fitting a linear equation to observed data.

When there is only one independent feature, it is known as Simple Linear Regression, and when there are more than one feature, it is known as Multiple Linear Regression.

Similarly, when there is only one dependent variable, it is considered Univariate Linear Regression, while when there are more than one dependent variables, it is known as Multivariate Regression.

Types of Linear Regression

There are two main types of linear regression:

Simple Linear Regression

This is the simplest form of linear regression, and it involves only one independent variable and one dependent variable. The equation for simple linear regression is:

$y={\beta }_0+{\beta }_{1}X$

where:

• y is the dependent variable
• X is the independent variable
• β0​ is the intercept
• β1 is the slope

Multiple Linear Regression

This involves more than one independent variable and one dependent variable. The equation for multiple linear regression is:

$y={\beta }_0+{\beta }_{1}X1+{\beta }_{2}X2+\dots \dots \dots {\beta }_{n}Xn$

where:

• Y is the dependent variable
• X1, X2, …, Xn are the independent variables
• β0 is the intercept
• β1, β2, …, βn are the slopes

The goal of the algorithm is to find the best Fit Line equation that can predict the values based on the independent variables.

In regression set of records are present with X and Y values and these values are used to learn a function so if you want to predict Y from an unknown X this learned function can be used. In regression we have to find the value of Y, So, a function is required that predicts continuous Y in the case of regression given X as independent features.

What is the best Fit Line?

Our primary objective while using linear regression is to locate the best-fit line, which implies that the error between the predicted and actual values should be kept to a minimum. There will be the least error in the best-fit line.

The best Fit Line equation provides a straight line that represents the relationship between the dependent and independent variables. The slope of the line indicates how much the dependent variable changes for a unit change in the independent variable(s).

The model gets the best regression fit line by finding the best θ1 and θ2 values. 

• θ1: intercept 
• θ2: coefficient of x 

Cost function for Linear Regression

The cost function or the loss function is nothing but the error or difference between the predicted value $\widehat{Y}$and the true value Y.

In Linear Regression, the Mean Squared Error (MSE) cost function is employed, which calculates the average of the squared errors between the predicted values ${\widehat{y}}_i$ and the actual values $y_i$. The purpose is to determine the optimal values for the intercept ${\theta }_1$ and the coefficient of the input feature ${\theta }_2$ providing the best-fit line for the given data points. The linear equation expressing this relationship is ${\widehat{y}}_i={\theta }_1+{\theta }_2{x}_i$.

MSE function can be calculated as:

$\text{Cost function}(J)=\frac{1}{n}{\sum }_n^i(\widehat{y_i}-y_i{)}^2$

Utilizing the MSE function, the iterative process of gradient descent is applied to update the values of  ${\theta }_1\mathrm{\&}{\theta }_2$. This ensures that the MSE value converges to the global minima, signifying the most accurate fit of the linear regression line to the dataset.

This process involves continuously adjusting the parameters based on the gradients calculated from the MSE. The final result is a linear regression line that minimizes the overall squared differences between the predicted and actual values, providing an optimal representation of the underlying relationship in the data.

Gradient Descent for Linear Regression

A linear regression model can be trained using the optimization algorithm gradient descent by iteratively modifying the model’s parameters to reduce the mean squared error (MSE) of the model on a training dataset. To update θ1 and θ2 values in order to reduce the Cost function (minimizing RMSE value) and achieve the best-fit line the model uses Gradient Descent. The idea is to start with random θ1 and θ2 values and then iteratively update the values, reaching minimum cost. 

A gradient is nothing but a derivative that defines the effects on outputs of the function with a little bit of variation in inputs.

Let’s differentiate the cost function(J) with respect to ${\theta }_1$

J’θ1​​​=∂θ1​∂J(θ1​,θ2​)​=∂θ1​∂​[n1​(i=1∑n​(y^​i​−yi​)2)]=n1​[i=1∑n​2(y^​i​−yi​)(∂θ1​∂​(y^​i​−yi​))]=n1​[i=1∑n​2(y^​i​−yi​)(∂θ1​∂​(θ1​+θ2​xi​−yi​))]=n1​[i=1∑n​2(y^​i​−yi​)(1+0−0)]=n1​[i=1∑n​(y^​i​−yi​)(2)]=n2​i=1∑n​(y^​i​−yi​)​

Let’s differentiate the cost function(J) with respect to ${\theta }_2$

$\begin{array}{rl}{\displaystyle J{\text{’}}_{{\theta }_2}}& {\displaystyle =\frac{\mathrm{\partial }J({\theta }_1,{\theta }_2)}{\mathrm{\partial }{\theta }_2}}\\ {\displaystyle }& {\displaystyle =\frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_2}\left[\frac{1}{n}(\sum _{i=1}^n({\widehat{y}}_i-y_i{)}^2)\right]}\\ {\displaystyle }& {\displaystyle =\frac{1}{n}[\sum _{i=1}^{n}2({\widehat{y}}_i-y_i)(\frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_2}({\widehat{y}}_i-y_i))]}\\ {\displaystyle }& {\displaystyle =\frac{1}{n}[\sum _{i=1}^{n}2({\widehat{y}}_i-y_i)(\frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_2}({\theta }_1+{\theta }_2{x}_i-y_i))]}\\ {\displaystyle }& {\displaystyle =\frac{1}{n}[\sum _{i=1}^{n}2({\widehat{y}}_i-y_i)(0+x_i-0)]}\\ {\displaystyle }& {\displaystyle =\frac{1}{n}[\sum _{i=1}^n({\widehat{y}}_i-y_i)\left(2x_i\right)]}\\ {\displaystyle }& {\displaystyle =\frac{2}{n}\sum _{i=1}^n({\widehat{y}}_i-y_i)\cdot x_i}\end{array}$

Finding the coefficients of a linear equation that best fits the training data is the objective of linear regression. By moving in the direction of the Mean Squared Error negative gradient with respect to the coefficients, the coefficients can be changed. And the respective intercept and coefficient of X will be if α is the learning rate.

θ1​​=θ1​–α(J’θ1​​)=θ1​−α(n2​i=1∑n​(y^​i​−yi​))​θ2​​=θ2​–α(J’θ2​​)=θ2​–α(n2​i=1∑n​(y^​i​−yi​)⋅xi​)​

Assumptions of Simple Linear Regression

Linear regression is a powerful tool for understanding and predicting the behavior of a variable, however, it needs to meet a few conditions in order to be accurate and dependable solutions. 

1. Linearity: The independent and dependent variables have a linear relationship with one another. This implies that changes in the dependent variable follow those in the independent variable(s) in a linear fashion. This means that there should be a straight line that can be drawn through the data points. If the relationship is not linear, then linear regression will not be an accurate model.
   
2. Independence: The observations in the dataset are independent of each other. This means that the value of the dependent variable for one observation does not depend on the value of the dependent variable for another observation. If the observations are not independent, then linear regression will not be an accurate model.
3. Homoscedasticity: Across all levels of the independent variable(s), the variance of the errors is constant. This indicates that the amount of the independent variable(s) has no impact on the variance of the errors. If the variance of the residuals is not constant, then linear regression will not be an accurate model.
   

   Homoscedasticity in Linear Regression

4. Normality: The residuals should be normally distributed. This means that the residuals should follow a bell-shaped curve. If the residuals are not normally distributed, then linear regression will not be an accurate model.

Assumptions of Multiple Linear Regression

For Multiple Linear Regression, all four of the assumptions from Simple Linear Regression apply. In addition to this, below are few more:

1. No multicollinearity: There is no high correlation between the independent variables. This indicates that there is little or no correlation between the independent variables. Multicollinearity occurs when two or more independent variables are highly correlated with each other, which can make it difficult to determine the individual effect of each variable on the dependent variable. If there is multicollinearity, then multiple linear regression will not be an accurate model.
2. Additivity: The model assumes that the effect of changes in a predictor variable on the response variable is consistent regardless of the values of the other variables. This assumption implies that there is no interaction between variables in their effects on the dependent variable.
3. Feature Selection: In multiple linear regression, it is essential to carefully select the independent variables that will be included in the model. Including irrelevant or redundant variables may lead to overfitting and complicate the interpretation of the model.
4. Overfitting: Overfitting occurs when the model fits the training data too closely, capturing noise or random fluctuations that do not represent the true underlying relationship between variables. This can lead to poor generalization performance on new, unseen data.

Multicollinearity

Multicollinearity is a statistical phenomenon that occurs when two or more independent variables in a multiple regression model are highly correlated, making it difficult to assess the individual effects of each variable on the dependent variable.

Detecting Multicollinearity includes two techniques:

• Correlation Matrix: Examining the correlation matrix among the independent variables is a common way to detect multicollinearity. High correlations (close to 1 or -1) indicate potential multicollinearity.
• VIF (Variance Inflation Factor): VIF is a measure that quantifies how much the variance of an estimated regression coefficient increases if your predictors are correlated. A high VIF (typically above 10) suggests multicollinearity.

K-Nearest Neighbors (KNN) algorithm

The K-Nearest Neighbors (KNN) algorithm is a supervised machine learning method employed to tackle classification and regression problems. 

KNN Algorithm working visualization

Why do we need a KNN algorithm?

(K-NN) algorithm is a versatile and widely used machine learning algorithm that is primarily used for its simplicity and ease of implementation. It does not require any assumptions about the underlying data distribution. It can also handle both numerical and categorical data, making it a flexible choice for various types of datasets in classification and regression tasks. It is a non-parametric method that makes predictions based on the similarity of data points in a given dataset. K-NN is less sensitive to outliers compared to other algorithms.

The K-NN algorithm works by finding the K nearest neighbors to a given data point based on a distance metric, such as Euclidean distance. The class or value of the data point is then determined by the majority vote or average of the K neighbors. This approach allows the algorithm to adapt to different patterns and make predictions based on the local structure of the data.

Distance Metrics Used in KNN Algorithm

we use below distance metrics:

Euclidean Distance

This is nothing but the cartesian distance between the two points which are in the plane/hyperplane. Euclidean distance can also be visualized as the length of the straight line that joins the two points which are into consideration. This metric helps us calculate the net displacement done between the two states of an object.

$\text{distance}(x,X_i)=\sqrt{{\sum }_{j=1}^d(x_j\text{–}{X}_{i_j}{)}^2}]$

Manhattan Distance

Manhattan Distance metric is generally used when we are interested in the total distance traveled by the object instead of the displacement. This metric is calculated by summing the absolute difference between the coordinates of the points in n-dimensions.

$d(x,y)={\sum }_{i=1}^n\mid x_i-y_i\mid$

Minkowski Distance

We can say that the Euclidean, as well as the Manhattan distance, are special cases of the Minkowski distance.

$d(x,y)={\left({\sum }_{i=1}^n{(x_i-y_i)}^p\right)}^{\frac{1}{p}}$

From the formula above we can say that when p = 2 then it is the same as the formula for the Euclidean distance and when p = 1 then we obtain the formula for the Manhattan distance.

The above-discussed metrics are most common while dealing with a Machine Learning problem but there are other distance metrics as well like Hamming Distance which come in handy while dealing with problems that require overlapping comparisons between two vectors whose contents can be Boolean as well as string values.

How to choose the value of k for KNN Algorithm?

The value of k is very crucial in the KNN algorithm to define the number of neighbors in the algorithm. The value of k in the k-nearest neighbors (k-NN) algorithm should be chosen based on the input data. If the input data has more outliers or noise, a higher value of k would be better. It is recommended to choose an odd value for k to avoid ties in classification. Cross-validation methods can help in selecting the best k value for the given dataset.

Algorithm for K-NN

DistanceToNN=sort(distance from 1st example, distance from kth example)

value i=1 to number of training records:

Dist=distance(test example, ith example)

if (Dist<any example in DistanceToNN):

Remove the example from DistanceToNN and value.

Put new example in DistanceToNN and value in sorted order.

Return average of value

Fit using K-NN is more reasonable than 1-NN, K-NN affects very less from noise if dataset is large.

In K-NN algorithm, We can see jump in prediction values due to unit change in input. The reason for this due to change in neighbors. To handles this situation, We can use weighting of neighbors in algorithm. If the distance from neighbor is high, we want less effect from that neighbor. If distance is low, that neighbor should be more effective than others.

Workings of KNN algorithm

Thе K-Nearest Neighbors (KNN) algorithm operates on the principle of similarity, where it predicts the label or value of a new data point by considering the labels or values of its K nearest neighbors in the training dataset.

Step-by-Step explanation of how KNN works is discussed below:

Step 1: Selecting the optimal value of K

• K represents the number of nearest neighbors that needs to be considered while making prediction.

Step 2: Calculating distance

• To measure the similarity between target and training data points, Euclidean distance is used. Distance is calculated between each of the data points in the dataset and target point.

Step 3: Finding Nearest Neighbors

• The k data points with the smallest distances to the target point are the nearest neighbors.

Step 4: Voting for Classification or Taking Average for Regression

• In the classification problem, the class labels of K-nearest neighbors are determined by performing majority voting. The class with the most occurrences among the neighbors becomes the predicted class for the target data point.
• In the regression problem, the class label is calculated by taking average of the target values of K nearest neighbors. The calculated average value becomes the predicted output for the target data point.

Let X be the training dataset with n data points, where each data point is represented by a d-dimensional feature vector $X_i$ and Y be the corresponding labels or values for each data point in X. Given a new data point x, the algorithm calculates the distance between x and each data point $X_i$ in X using a distance metric, such as Euclidean distance:$\text{distance}(x,X_i)=\sqrt{{\sum }_{j=1}^d(x_j\text{–}{X}_{i_j}{)}^2}]$

The algorithm selects the K data points from X that have the shortest distances to x. For classification tasks, the algorithm assigns the label y that is most frequent among the K nearest neighbors to x. For regression tasks, the algorithm calculates the average or weighted average of the values y of the K nearest neighbors and assigns it as the predicted value for x.

Advantages of the KNN Algorithm

• Easy to implement as the complexity of the algorithm is not that high.
• Adapts Easily – As per the working of the KNN algorithm it stores all the data in memory storage and hence whenever a new example or data point is added then the algorithm adjusts itself as per that new example and has its contribution to the future predictions as well.
• Few Hyperparameters – The only parameters which are required in the training of a KNN algorithm are the value of k and the choice of the distance metric which we would like to choose from our evaluation metric.

Disadvantages of the KNN Algorithm

• Does not scale – As we have heard about this that the KNN algorithm is also considered a Lazy Algorithm. The main significance of this term is that this takes lots of computing power as well as data storage. This makes this algorithm both time-consuming and resource exhausting.
• Curse of Dimensionality – There is a term known as the peaking phenomenon according to this the KNN algorithm is affected by the curse of dimensionality which implies the algorithm faces a hard time classifying the data points properly when the dimensionality is too high.
• Prone to Overfitting – As the algorithm is affected due to the curse of dimensionality it is prone to the problem of overfitting as well. Hence generally feature selection as well as dimensionality reduction techniques are applied to deal with this problem.
• Applications of the KNN Algorithm

• Data Preprocessing – While dealing with any Machine Learning problem we first perform the EDA part in which if we find that the data contains missing values then there are multiple imputation methods are available as well. One of such method is KNN Imputer which is quite effective ad generally used for sophisticated imputation methodologies.
• Pattern Recognition – KNN algorithms work very well if you have trained a KNN algorithm using the MNIST dataset and then performed the evaluation process then you must have come across the fact that the accuracy is too high.
• Recommendation Engines – The main task which is performed by a KNN algorithm is to assign a new query point to a pre-existed group that has been created using a huge corpus of datasets. This is exactly what is required in the recommender systems to assign each user to a particular group and then provide them recommendations based on that group’s preferences.

Logistic Regression

Logistic regression is a supervised machine learning algorithm used for classification tasks where the goal is to predict the probability that an instance belongs to a given class or not. Logistic regression is a statistical algorithm which analyze the relationship between two data factors.

Logistic Function – Sigmoid Function

• The sigmoid function is a mathematical function used to map the predicted values to probabilities.
• It maps any real value into another value within a range of 0 and 1. The value of the logistic regression must be between 0 and 1, which cannot go beyond this limit, so it forms a curve like the “S” form.
• The S-form curve is called the Sigmoid function or the logistic function.
• In logistic regression, we use the concept of the threshold value, which defines the probability of either 0 or 1. Such as values above the threshold value tends to 1, and a value below the threshold values tends to 0.

Types of Logistic Regression

On the basis of the categories, Logistic Regression can be classified into three types:

1. Binomial: In binomial Logistic regression, there can be only two possible types of the dependent variables, such as 0 or 1, Pass or Fail, etc.
2. Multinomial: In multinomial Logistic regression, there can be 3 or more possible unordered types of the dependent variable, such as “cat”, “dogs”, or “sheep”
3. Ordinal: In ordinal Logistic regression, there can be 3 or more possible ordered types of dependent variables, such as “low”, “Medium”, or “High”.

Assumptions of Logistic Regression

We will explore the assumptions of logistic regression as understanding these assumptions is important to ensure that we are using appropriate application of the model. The assumption include:

1. Independent observations: Each observation is independent of the other. meaning there is no correlation between any input variables.
2. Binary dependent variables: It takes the assumption that the dependent variable must be binary or dichotomous, meaning it can take only two values. For more than two categories SoftMax functions are used.
3. Linearity relationship between independent variables and log odds: The relationship between the independent variables and the log odds of the dependent variable should be linear.
4. No outliers: There should be no outliers in the dataset.
5. Large sample size: The sample size is sufficiently large

Terminologies involved in Logistic Regression

Here are some common terms involved in logistic regression:

• Independent variables: The input characteristics or predictor factors applied to the dependent variable’s predictions.
• Dependent variable: The target variable in a logistic regression model, which we are trying to predict.
• Logistic function: The formula used to represent how the independent and dependent variables relate to one another. The logistic function transforms the input variables into a probability value between 0 and 1, which represents the likelihood of the dependent variable being 1 or 0.
• Odds: It is the ratio of something occurring to something not occurring. it is different from probability as the probability is the ratio of something occurring to everything that could possibly occur.
• Log-odds: The log-odds, also known as the logit function, is the natural logarithm of the odds. In logistic regression, the log odds of the dependent variable are modeled as a linear combination of the independent variables and the intercept.
• Coefficient: The logistic regression model’s estimated parameters, show how the independent and dependent variables relate to one another.
• Intercept: A constant term in the logistic regression model, which represents the log odds when all independent variables are equal to zero.
• Maximum likelihood estimation: The method used to estimate the coefficients of the logistic regression model, which maximizes the likelihood of observing the data given the model.

How does Logistic Regression work?

The logistic regression model transforms the linear regression function continuous value output into categorical value output using a sigmoid function, which maps any real-valued set of independent variables input into a value between 0 and 1. This function is known as the logistic function.

Let the independent input features be:

  

 and the dependent variable is Y having only binary value i.e. 0 or 1. 

$Y=\{\begin{array}{ll}0& \text{ if }Class1\\ 1& \text{ if }Class2\end{array}$

then, apply the multi-linear function to the input variables X.

$z=\left({\sum }_{i=1}^n{w}_i{x}_i\right)+b$

Here $x_i$ is the ith observation of X, $w_i=[w_1,w_2,w_3,\cdots ,w_m]$ is the weights or Coefficient, and b is the bias term also known as intercept. simply this can be represented as the dot product of weight and bias.

$z=w\cdot X+b$

whatever we discussed above is the linear regression. 

Sigmoid Function

Now we use the sigmoid function where the input will be z and we find the probability between 0 and 1. i.e. predicted y.

$\sigma (z)=\frac{1}{1+e^{-z}}$

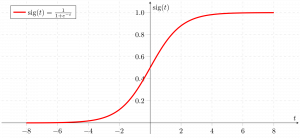
Sigmoid function

As shown above, the figure sigmoid function converts the continuous variable data into the probability i.e. between 0 and 1. 

• $\sigma (z)$ tends towards 1 as $z\to \mathrm{\infty }$
• $\sigma (z)$ tends towards 0 as $z\to -\mathrm{\infty }$
• $\sigma (z)$ is always bounded between 0 and 1

where the probability of being a class can be measured as:

$$\begin{gathered} P(y=1)=\sigma (z) \\ P(y=0)=1-\sigma (z) \end{gathered}$$

Logistic Regression Equation

The odd is the ratio of something occurring to something not occurring. it is different from probability as the probability is the ratio of something occurring to everything that could possibly occur. so odd will be:

$\frac{p(x)}{1-p(x)}=e^z$

Applying natural log on odd. then log odd will be:

$\begin{array}{rl}{\displaystyle \log \left[\frac{p(x)}{1-p(x)}\right]}& {\displaystyle =z}\\ {\displaystyle \log \left[\frac{p(x)}{1-p(x)}\right]}& {\displaystyle =w\cdot X+b}\\ {\displaystyle \frac{p(x)}{1-p(x)}}& {\displaystyle =e^{w\cdot X+b}\cdots \text{Exponentiate both sides}}\\ {\displaystyle p(x)}& {\displaystyle =e^{w\cdot X+b}\cdot (1-p(x))}\\ {\displaystyle p(x)}& {\displaystyle =e^{w\cdot X+b}-e^{w\cdot X+b}\cdot p(x))}\\ {\displaystyle p(x)+e^{w\cdot X+b}\cdot p(x))}& {\displaystyle =e^{w\cdot X+b}}\\ {\displaystyle p(x)(1+e^{w\cdot X+b})}& {\displaystyle =e^{w\cdot X+b}}\\ {\displaystyle p(x)}& {\displaystyle =\frac{e^{w\cdot X+b}}{1+e^{w\cdot X+b}}}\end{array}$

then the final logistic regression equation will be:

$p(X;b,w)=\frac{e^{w\cdot X+b}}{1+e^{w\cdot X+b}}=\frac{1}{1+e^{-w\cdot X+b}}$

Likelihood Function for Logistic Regression

The predicted probabilities will be:

• for y=1 The predicted probabilities will be: p(X;b,w) = p(x)
• for y = 0 The predicted probabilities will be: 1-p(X;b,w) = 1-p(x)

$L(b,w)={\prod }_{i=1}^{n}p(x_i{)}^{y_i}(1-p(x_i){)}^{1-y_i}$

Taking natural logs on both sides

$\begin{array}{rl}{\displaystyle \log (L(b,w))}& {\displaystyle =\sum _{i=1}^n{y}_i\log p(x_i)+(1-y_i)\log (1-p(x_i))}\\ {\displaystyle }& {\displaystyle =\sum _{i=1}^n{y}_i\log p(x_i)+\log (1-p(x_i))-y_i\log (1-p(x_i))}\\ {\displaystyle }& {\displaystyle =\sum _{i=1}^n\log (1-p(x_i))+\sum _{i=1}^n{y}_i\log \frac{p(x_i)}{1-p(x_i}}\\ {\displaystyle }& {\displaystyle =\sum _{i=1}^n-\log 1-e^{-(w\cdot x_i+b)}+\sum _{i=1}^n{y}_i(w\cdot x_i+b)}\\ {\displaystyle }& {\displaystyle =\sum _{i=1}^n-\log 1+e^{w\cdot x_i+b}+\sum _{i=1}^n{y}_i(w\cdot x_i+b)}\end{array}$

Gradient of the log-likelihood function

To find the maximum likelihood estimates, we differentiate w.r.t w,

$\begin{array}{rl}{\displaystyle \frac{\mathrm{\partial }J(l(b,w)}{\mathrm{\partial }{w}_j}}& {\displaystyle =-\sum _{i=n}^n\frac{1}{1+e^{w\cdot x_i+b}}{e}^{w\cdot x_i+b}{x}_{ij}+\sum _{i=1}^n{y}_i{x}_{ij}}\\ {\displaystyle }& {\displaystyle =-\sum _{i=n}^{n}p(x_i;b,w)x_{ij}+\sum _{i=1}^n{y}_i{x}_{ij}}\\ {\displaystyle }& {\displaystyle =\sum _{i=n}^n(y_i-p(x_i;b,w))x_{ij}}\end{array}$

Neural Networks

Neural Networks are computational models that mimic the complex functions of the human brain. The neural networks consist of interconnected nodes or neurons that process and learn from data, enabling tasks such as pattern recognition and decision making in machine learning.

What are Neural Networks?

Neural networks extract identifying features from data, lacking pre-programmed understanding. Network components include neurons, connections, weights, biases, propagation functions, and a learning rule. Neurons receive inputs, governed by thresholds and activation functions. Connections involve weights and biases regulating information transfer. Learning, adjusting weights and biases, occurs in three stages: input computation, output generation, and iterative refinement enhancing the network’s proficiency in diverse tasks.

These include:

1. The neural network is simulated by a new environment.
2. Then the free parameters of the neural network are changed as a result of this simulation.
3. The neural network then responds in a new way to the environment because of the changes in its free parameters.

Working of a Neural Network

Neural networks are complex systems that mimic some features of the functioning of the human brain. It is composed of an input layer, one or more hidden layers, and an output layer made up of layers of artificial neurons that are coupled. The two stages of the basic process are called backpropagation and forward propagation.

Forward Propagation

• Input Layer: Each feature in the input layer is represented by a node on the network, which receives input data.
• Weights and Connections: The weight of each neuronal connection indicates how strong the connection is. Throughout training, these weights are changed.
• Hidden Layers: Each hidden layer neuron processes inputs by multiplying them by weights, adding them up, and then passing them through an activation function. By doing this, non-linearity is introduced, enabling the network to recognize intricate patterns.
• Output: The final result is produced by repeating the process until the output layer is reached.

Backpropagation

• Loss Calculation: The network’s output is evaluated against the real goal values, and a loss function is used to compute the difference. For a regression problem, the Mean Squared Error (MSE) is commonly used as the cost function.
  Loss Function:
  
• Gradient Descent: Gradient descent is then used by the network to reduce the loss. To lower the inaccuracy, weights are changed based on the derivative of the loss with respect to each weight.
• Adjusting weights: The weights are adjusted at each connection by applying this iterative process, or backpropagation, backward across the network.
• Training: During training with different data samples, the entire process of forward propagation, loss calculation, and backpropagation is done iteratively, enabling the network to adapt and learn patterns from the data.
• Activation Functions: Model non-linearity is introduced by activation functions like the rectified linear unit (ReLU) or sigmoid. Their decision on whether to “fire” a neuron is based on the whole weighted input.

Types of Neural Networks

There are seven types of neural networks that can be used.

• Feedforward Neteworks: A feedforward neural network is a simple artificial neural network architecture in which data moves from input to output in a single direction. It has input, hidden, and output layers; feedback loops are absent. Its straightforward architecture makes it appropriate for a number of applications, such as regression and pattern recognition.
• Multilayer Perceptron (MLP): MLP is a type of feedforward neural network with three or more layers, including an input layer, one or more hidden layers, and an output layer. It uses nonlinear activation functions.
• Convolutional Neural Network (CNN): A Convolutional Neural Network (CNN) is a specialized artificial neural network designed for image processing. It employs convolutional layers to automatically learn hierarchical features from input images, enabling effective image recognition and classification. CNNs have revolutionized computer vision and are pivotal in tasks like object detection and image analysis.
• Recurrent Neural Network (RNN): An artificial neural network type intended for sequential data processing is called a Recurrent Neural Network (RNN). It is appropriate for applications where contextual dependencies are critical, such as time series prediction and natural language processing, since it makes use of feedback loops, which enable information to survive within the network.
• Long Short-Term Memory (LSTM): LSTM is a type of RNN that is designed to overcome the vanishing gradient problem in training RNNs. It uses memory cells and gates to selectively read, write, and erase information.

Advantages of Neural Networks

Neural networks are widely used in many different applications because of their many benefits:

• Adaptability: Neural networks are useful for activities where the link between inputs and outputs is complex or not well defined because they can adapt to new situations and learn from data.
• Pattern Recognition: Their proficiency in pattern recognition renders them efficacious in tasks like as audio and image identification, natural language processing, and other intricate data patterns.
• Parallel Processing: Because neural networks are capable of parallel processing by nature, they can process numerous jobs at once, which speeds up and improves the efficiency of computations.
• Non-Linearity: Neural networks are able to model and comprehend complicated relationships in data by virtue of the non-linear activation functions found in neurons, which overcome the drawbacks of linear models.

Disadvantages of Neural Networks

Neural networks, while powerful, are not without drawbacks and difficulties:

• Computational Intensity: Large neural network training can be a laborious and computationally demanding process that demands a lot of computing power.
• Black box Nature: As “black box” models, neural networks pose a problem in important applications since it is difficult to understand how they make decisions.
• Overfitting: Overfitting is a phenomenon in which neural networks commit training material to memory rather than identifying patterns in the data. Although regularization approaches help to alleviate this, the problem still exists.
• Need for Large datasets: For efficient training, neural networks frequently need sizable, labeled datasets; otherwise, their performance may suffer from incomplete or skewed data.

Module 5

Evaluation Metrics for Classification Task

In this Python code, we have imported the iris dataset which has features like the length and width of sepals and petals. The target values are Iris setosa, Iris virginica, and Iris versicolor. After importing the dataset we divided the dataset into train and test datasets in the ratio 80:20. Then we called Decision Trees and trained our model. After that, we performed the prediction and calculated the accuracy score, precision, recall, and f1 score. We also plotted the confusion matrix.

Importing Libraries and Dataset

Python libraries make it very easy for us to handle the data and perform typical and complex tasks with a single line of code.

Pandas – This library helps to load the data frame in a 2D array format and has multiple functions to perform analysis tasks in one go.

Numpy – Numpy arrays are very fast and can perform large computations in a very short time.

Matplotlib/Seaborn – This library is used to draw visualizations.

Sklearn – This module contains multiple libraries having pre-implemented functions to perform tasks from data preprocessing to model development and evaluation.

import pandas as pd 

import numpy as np 

from sklearn import tree 

from sklearn import datasets 

from sklearn.datasets import load_iris 

from sklearn.tree import DecisionTreeClassifier 

from sklearn.model_selection import train_test_split 

import seaborn as sns 

import matplotlib.pyplot as plt 

from sklearn.metrics import precision_score, recall_score, f1_score, accuracy_score

Now let’s load the toy dataset iris flowers from the sklearn.datasets library and then split it into training and testing parts (for model evaluation) in the 80:20 ratio.

iris = load_iris() 

X = iris.data 

y = iris.target 

  

# Holdout method.Dividing the data into train and test 

X_train, X_test,\ 

    y_train, y_test = train_test_split(X, y, 

                                       random_state=20, 

                                       test_size=0.20) 

Now, let’s train a Decision Tree Classifier model on the training data, and then we will move on to the evaluation part of the model using different metrics.

tree = DecisionTreeClassifier()

tree.fit(X_train, y_train)

y_pred = tree.predict(X_test)

Accuracy

Accuracy is defined as the ratio of the number of correct predictions to the total number of predictions. This is the most fundamental metric used to evaluate the model. The formula is given by

Accuracy = (TP+TN)/(TP+TN+FP+FN)

However, Accuracy has a drawback. It cannot perform well on an imbalanced dataset. Suppose a model classifies that the majority of the data belongs to the major class label. It yields higher accuracy. But in general, the model cannot classify on minor class labels and has poor performance.

print("Accuracy:", accuracy_score(y_test, y_pred)) 

Output:

Accuracy: 0.9333333333333333

Precision and Recall

Precision is the ratio of true positives to the summation of true positives and false positives. It basically analyses the positive predictions.

Precision = TP/(TP+FP)

The drawback of Precision is that it does not consider the True  Negatives and False Negatives.

Recall is the ratio of true positives to the summation of true positives and false negatives. It basically analyses the number of correct positive samples.

Recall = TP/(TP+FN)

The drawback of Recall is that often it leads to a higher false positive rate.

print("Precision:", precision_score(y_test, y_pred, average="weighted")) print('Recall:', recall_score(y_test, y_pred, average="weighted")) 

Output:

Precision: 0.9435897435897436

Recall: 0.9333333333333333

F1 score

The F1 score is the harmonic mean of precision and recall. It is seen that during the precision-recall trade-off if we increase the precision, recall decreases and vice versa. The goal of the F1 score is to combine precision and recall. 

F1 score = (2×Precision×Recall)/(Precision+Recall)

# calculating f1 score 

print('F1 score:', f1_score(y_test, y_pred, average="weighted")) 

Output:

F1 score: 0.9327777777777778

Confusion Matrix

A confusion matrix is an N x N matrix where N is the number of target classes. It represents the number of actual outputs and the predicted outputs. Some terminologies in the matrix are as follows:

True Positives: It is also known as TP. It is the output in which the actual and the predicted values are YES.

True Negatives:  It is also known as TN. It is the output in which the actual and the predicted values are NO.

False Positives: It is also known as FP. It is the output in which the actual value is NO but the predicted value is YES.

False Negatives:  It is also known as FN. It is the output in which the actual value is YES but the predicted value is NO.

confusion_matrix = metrics.confusion_matrix(y_test, y_pred) 

  

cm_display=metrics.ConfusionMatrixDisplay( confusion_matrix=confusion_matrix, display_labels=[0, 1, 2]) 

  

cm_display.plot() 

plt.show()

In the output, the accuracy of the model is 93.33%. Precision is approximately 0.944  and Recall is 0.933. F1 score is approximately 0.933. Finally, the confusion matrix is plotted. Here class labels denote the target classes: 

0 = Setosa

1 = Versicolor

2 = Virginica

From the confusion matrix, we see that 8 setosa classes were correctly predicted. 11 Versicolor test cases were also correctly predicted by the model and 2 virginica test cases were misclassified. In contrast, the rest 9 were correctly predicted.

AUC-ROC Curve

AUC (Area Under Curve) is an evaluation metric that is used to analyze the classification model at different threshold values. The Receiver Operating Characteristic(ROC) curve is a probabilistic curve used to highlight the model’s performance. The curve has two parameters:

TPR: It stands for True positive rate. It basically follows the formula of Recall.

FPR: It stands for False Positive rate. It is defined as the ratio of False positives to the summation of false positives and True negatives.

This curve is useful as it helps us to determine the model’s capacity to distinguish between different classes. Let us illustrate this with the help of a simple Python example

import numpy as np 

from sklearn .metrics import roc_auc_score 

y_true = [1, 0, 0, 1] 

y_pred = [1, 0, 0.9, 0.2] 

auc = np.round(roc_auc_score(y_true, y_pred), 3) 

print("Auc", (auc)) 

Output:

Auc 0.75

AUC score is a useful metric to evaluate the model. It basically highlights a model’s capacity to separate the classes. In the above code, 0.75 is a good AUC score. A model is considered good if the AUC score is greater than 0.5 and approaches 1. A poor model has an AUC score of 0.

Evaluation Metrics for Regression Task

Regression is used to determine continuous values. It is mostly used to find a relation between a dependent and an independent variable. For classification, we use a confusion matrix, accuracy, f1 score, etc. But for regression analysis, since we are predicting a numerical value it may differ from the actual output.  So we consider the error calculation as it helps to summarize how close the prediction is to the actual value. There are many metrics available for evaluating the regression model.

In this Python Code, we have implemented a simple regression model using the Mumbai weather CSV file. This file comprises Day, Hour, Temperature, Relative Humidity, Wind Speed, and Wind Direction. The link for the dataset is here.

 We are basically interested in finding a relationship between Temperature and Relative Humidity. Here Relative Humidity is the dependent variable and Temperature is the independent variable. We performed the Linear Regression and used the metrics to evaluate the performance of our model. To calculate the metrics we make extensive use of sklearn library.

# importing the libraries 

from sklearn.linear_model import LinearRegression 

from sklearn.metrics import mean_absolute_error,\ mean_squared_error, mean_absolute_percentage_error 

Now let’s load the data into the panda’s data frame and then split it into training and testing parts (for model evaluation) in the 80:20 ratio.

df = pd.read_csv('weather.csv') 

X = df.iloc[:, 2].values 

Y = df.iloc[:, 3].values 

X_train, X_test,\ Y_train, Y_test = train_test_split(X, Y, test_size=0.20, random_state=0) 

Now, let’s train a simple linear regression model. On the training data and we will move to the evaluation part of the model using different metrics.

X_train = X_train.reshape(-1, 1) 

X_test = X_test.reshape(-1, 1) 

regression = LinearRegression() 

regression.fit(X_train, Y_train) 

Y_pred = regression.predict(X_test)

Mean Absolute Error(MAE)

This is the simplest metric used to analyze the loss over the whole dataset. As we all know the error is basically the difference between the predicted and actual values. Therefore MAE is defined as the average of the errors calculated. Here we calculate the modulus of the error, perform the summation and then divide the result by the number of data points.  It is a positive quantity and is not concerned about the direction. The formula of MAE is given by

MAE = ∑|ypred-yactual| / N

mae = mean_absolute_error(y_true=Y_test, y_pred=Y_pred) 

print("Mean Absolute Error", mae) 

Output:

Mean Absolute Error 1.7236295632503873

Mean Squared Error(MSE)

The most commonly used metric is Mean Square error or MSE. It is a function used to calculate the loss. We find the difference between the predicted values and the truth variable, square the result and then find the average over the whole dataset. MSE is always positive as we square the values. The small the MSE better is the performance of our model. The formula of MSE is given:

MSE = ∑(ypred - yactual)2 / N

mse = mean_squared_error(y_true=Y_test, y_pred=Y_pred) 

print("Mean Square Error", mse)

Output:

Mean Square Error 3.9808057060106954

Root Mean Squared Error(RMSE)

RMSE is a popular method and is the extended version of MSE(Mean Squared Error). This method is basically used to evaluate the performance of our model. It indicates how much the data points are spread around the best line. It is the standard deviation of the Mean squared error. A lower value means that the data point lies closer to the best fit line.

RMSE=√(∑(ypred - yactual)2 / N)

rmse = mean_squared_error(y_true=Y_test, y_pred=Y_pred, 

                          squared=False) 

print("Root Mean Square Error", rmse) 

Output:

Root Mean Square Error 1.9951956560725306